In his very young years the hero of our story, king Copa, decided that his private data was hidden not enough securely, what is unacceptable for the king. That's why he invented tricky and clever password (later he learned that his password is a palindrome of odd length), and coded all his data using it.
Copa is afraid to forget his password, so he decided to write it on a piece of paper. He is aware that it is insecure to keep password in such way, so he decided to cipher it the following way: he cut x characters from the start of his password and from the end of it (x can be 0, and 2x is strictly less than the password length). He obtained 3 parts of the password. Let's call it prefix, middle and suffix correspondingly, both prefix and suffix having equal length and middle always having odd length. From these parts he made a string A + prefix + B + middle + C + suffix, where A, B and C are some (possibly empty) strings invented by Copa, and « + » means concatenation.
Many years have passed, and just yesterday the king Copa found the piece of paper where his ciphered password was written. The password, as well as the strings A, B and C, was completely forgotten by Copa, so he asks you to find a password of maximum possible length, which could be invented, ciphered and written by Copa.
The input contains single string of small Latin letters with length from 1 to 105 characters.
The first line should contain integer k — amount of nonempty parts of the password in your answer (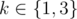 ). In each of the following k lines output two integers xi and li — start and length of the corresponding part of the password. Output pairs in order of increasing xi. Separate the numbers in pairs by a single space.
). In each of the following k lines output two integers xi and li — start and length of the corresponding part of the password. Output pairs in order of increasing xi. Separate the numbers in pairs by a single space.
Starting position xi should be an integer from 1 to the length of the input string. All li must be positive, because you should output only non-empty parts. The middle part must have odd length.
If there are several solutions, output any. Note that your goal is to maximize the sum of li, but not to maximize k.
abacaba
1
1 7
axbya
3
1 1
2 1
5 1
xabyczba
3
2 2
4 1
7 2
| Name |
|---|




