| Codeforces Round 210 (Div. 1) |
|---|
| Finished |
Levko loves array a1, a2, ... , an, consisting of integers, very much. That is why Levko is playing with array a, performing all sorts of operations with it. Each operation Levko performs is of one of two types:
- Increase all elements from li to ri by di. In other words, perform assignments aj = aj + di for all j that meet the inequation li ≤ j ≤ ri.
- Find the maximum of elements from li to ri. That is, calculate the value
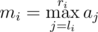 .
.
Sadly, Levko has recently lost his array. Fortunately, Levko has records of all operations he has performed on array a. Help Levko, given the operation records, find at least one suitable array. The results of all operations for the given array must coincide with the record results. Levko clearly remembers that all numbers in his array didn't exceed 109 in their absolute value, so he asks you to find such an array.
The first line contains two integers n and m (1 ≤ n, m ≤ 5000) — the size of the array and the number of operations in Levko's records, correspondingly.
Next m lines describe the operations, the i-th line describes the i-th operation. The first integer in the i-th line is integer ti (1 ≤ ti ≤ 2) that describes the operation type. If ti = 1, then it is followed by three integers li, ri and di (1 ≤ li ≤ ri ≤ n, - 104 ≤ di ≤ 104) — the description of the operation of the first type. If ti = 2, then it is followed by three integers li, ri and mi (1 ≤ li ≤ ri ≤ n, - 5·107 ≤ mi ≤ 5·107) — the description of the operation of the second type.
The operations are given in the order Levko performed them on his array.
In the first line print "YES" (without the quotes), if the solution exists and "NO" (without the quotes) otherwise.
If the solution exists, then on the second line print n integers a1, a2, ... , an (|ai| ≤ 109) — the recovered array.
4 5
1 2 3 1
2 1 2 8
2 3 4 7
1 1 3 3
2 3 4 8
YES
4 7 4 7
4 5
1 2 3 1
2 1 2 8
2 3 4 7
1 1 3 3
2 3 4 13
NO
| Name |
|---|




