| Codeforces Round 278 (Div. 1) |
|---|
| Finished |
There are n cities in Cyberland, numbered from 1 to n, connected by m bidirectional roads. The j-th road connects city aj and bj.
For tourists, souvenirs are sold in every city of Cyberland. In particular, city i sell it at a price of wi.
Now there are q queries for you to handle. There are two types of queries:
- "C a w": The price in city a is changed to w.
- "A a b": Now a tourist will travel from city a to b. He will choose a route, he also doesn't want to visit a city twice. He will buy souvenirs at the city where the souvenirs are the cheapest (possibly exactly at city a or b). You should output the minimum possible price that he can buy the souvenirs during his travel.
More formally, we can define routes as follow:
- A route is a sequence of cities [x1, x2, ..., xk], where k is a certain positive integer.
- For any 1 ≤ i < j ≤ k, xi ≠ xj.
- For any 1 ≤ i < k, there is a road connecting xi and xi + 1.
- The minimum price of the route is min(wx1, wx2, ..., wxk).
- The required answer is the minimum value of the minimum prices of all valid routes from a to b.
The first line of input contains three integers n, m, q (1 ≤ n, m, q ≤ 105), separated by a single space.
Next n lines contain integers wi (1 ≤ wi ≤ 109).
Next m lines contain pairs of space-separated integers aj and bj (1 ≤ aj, bj ≤ n, aj ≠ bj).
It is guaranteed that there is at most one road connecting the same pair of cities. There is always at least one valid route between any two cities.
Next q lines each describe a query. The format is "C a w" or "A a b" (1 ≤ a, b ≤ n, 1 ≤ w ≤ 109).
For each query of type "A", output the corresponding answer.
3 3 3
1
2
3
1 2
2 3
1 3
A 2 3
C 1 5
A 2 3
1
2
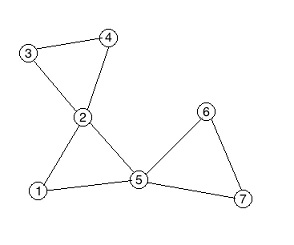
7 9 4
1
2
3
4
5
6
7
1 2
2 5
1 5
2 3
3 4
2 4
5 6
6 7
5 7
A 2 3
A 6 4
A 6 7
A 3 3
2
1
5
3
For the second sample, an optimal routes are:
From 2 to 3 it is [2, 3].
From 6 to 4 it is [6, 5, 1, 2, 4].
From 6 to 7 it is [6, 5, 7].
From 3 to 3 it is [3].
| Name |
|---|




