| Codeforces Round 313 (Div. 1) |
|---|
| Finished |
Gerald got tired of playing board games with the usual six-sided die, and he bought a toy called Randomizer. It functions as follows.
A Randomizer has its own coordinate plane on which a strictly convex polygon is painted, the polygon is called a basic polygon. If you shake a Randomizer, it draws some nondegenerate (i.e. having a non-zero area) convex polygon with vertices at some vertices of the basic polygon. The result of the roll (more precisely, the result of the shaking) is considered to be the number of points with integer coordinates, which were strictly inside (the points on the border are not considered) the selected polygon. Now Gerald is wondering: what is the expected result of shaking the Randomizer?
During the shaking the Randomizer considers all the possible non-degenerate convex polygons with vertices at the vertices of the basic polygon. Let's assume that there are k versions of the polygons. Then the Randomizer chooses each of them with probability  .
.
The first line of the input contains a single integer n (3 ≤ n ≤ 100 000) — the number of vertices of the basic polygon.
Next n lines contain the coordinates of the vertices of the basic polygon. The i-th of these lines contain two integers xi and yi ( - 109 ≤ xi, yi ≤ 109) — the coordinates of the i-th vertex of the polygon. The vertices are given in the counter-clockwise order.
Print the sought expected value with absolute or relative error at most 10 - 9.
4
0 0
2 0
2 2
0 2
0.2
5
0 0
2 0
2 2
1 3
0 2
0.8125
A polygon is called strictly convex if it is convex and no its vertices lie on the same line.
Let's assume that a random variable takes values x1, ..., xn with probabilities p1, ..., pn, correspondingly. Then the expected value of this variable equals to 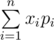 .
.
| Name |
|---|




