| Codeforces Round 330 (Div. 1) |
|---|
| Finished |
Today on a math lesson the teacher told Vovochka that the Euler function of a positive integer φ(n) is an arithmetic function that counts the positive integers less than or equal to n that are relatively prime to n. The number 1 is coprime to all the positive integers and φ(1) = 1.
Now the teacher gave Vovochka an array of n positive integers a1, a2, ..., an and a task to process q queries li ri — to calculate and print 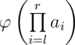 modulo 109 + 7. As it is too hard for a second grade school student, you've decided to help Vovochka.
modulo 109 + 7. As it is too hard for a second grade school student, you've decided to help Vovochka.
The first line of the input contains number n (1 ≤ n ≤ 200 000) — the length of the array given to Vovochka. The second line contains n integers a1, a2, ..., an (1 ≤ ai ≤ 106).
The third line contains integer q (1 ≤ q ≤ 200 000) — the number of queries. Next q lines contain the queries, one per line. Each query is defined by the boundaries of the segment li and ri (1 ≤ li ≤ ri ≤ n).
Print q numbers — the value of the Euler function for each query, calculated modulo 109 + 7.
10
1 2 3 4 5 6 7 8 9 10
7
1 1
3 8
5 6
4 8
8 10
7 9
7 10
1
4608
8
1536
192
144
1152
7
24 63 13 52 6 10 1
6
3 5
4 7
1 7
2 4
3 6
2 6
1248
768
12939264
11232
9984
539136
In the second sample the values are calculated like that:
- φ(13·52·6) = φ(4056) = 1248
- φ(52·6·10·1) = φ(3120) = 768
- φ(24·63·13·52·6·10·1) = φ(61326720) = 12939264
- φ(63·13·52) = φ(42588) = 11232
- φ(13·52·6·10) = φ(40560) = 9984
- φ(63·13·52·6·10) = φ(2555280) = 539136
| Name |
|---|




