| Codeforces Round 372 (Div. 1) |
|---|
| Finished |
ZS the Coder is given two permutations p and q of {1, 2, ..., n}, but some of their elements are replaced with 0. The distance between two permutations p and q is defined as the minimum number of moves required to turn p into q. A move consists of swapping exactly 2 elements of p.
ZS the Coder wants to determine the number of ways to replace the zeros with positive integers from the set {1, 2, ..., n} such that p and q are permutations of {1, 2, ..., n} and the distance between p and q is exactly k.
ZS the Coder wants to find the answer for all 0 ≤ k ≤ n - 1. Can you help him?
The first line of the input contains a single integer n (1 ≤ n ≤ 250) — the number of elements in the permutations.
The second line contains n integers, p1, p2, ..., pn (0 ≤ pi ≤ n) — the permutation p. It is guaranteed that there is at least one way to replace zeros such that p is a permutation of {1, 2, ..., n}.
The third line contains n integers, q1, q2, ..., qn (0 ≤ qi ≤ n) — the permutation q. It is guaranteed that there is at least one way to replace zeros such that q is a permutation of {1, 2, ..., n}.
Print n integers, i-th of them should denote the answer for k = i - 1. Since the answer may be quite large, and ZS the Coder loves weird primes, print them modulo 998244353 = 223·7·17 + 1, which is a prime.
3
1 0 0
0 2 0
1 2 1
4
1 0 0 3
0 0 0 4
0 2 6 4
6
1 3 2 5 4 6
6 4 5 1 0 0
0 0 0 0 1 1
4
1 2 3 4
2 3 4 1
0 0 0 1
In the first sample case, there is the only way to replace zeros so that it takes 0 swaps to convert p into q, namely p = (1, 2, 3), q = (1, 2, 3).
There are two ways to replace zeros so that it takes 1 swap to turn p into q. One of these ways is p = (1, 2, 3), q = (3, 2, 1), then swapping 1 and 3 from p transform it into q. The other way is p = (1, 3, 2), q = (1, 2, 3). Swapping 2 and 3 works in this case.
Finally, there is one way to replace zeros so that it takes 2 swaps to turn p into q, namely p = (1, 3, 2), q = (3, 2, 1). Then, we can transform p into q like following: 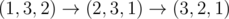 .
.
| Name |
|---|




