Шерлок нашел зашифрованые данные, которые, как он считает, могут помочь поймать Мориарти. Зашифрованные данные состоят из двух целых чисел l и r. Шерлок заметил, что эти числа записаны в шестнадцатеричной системе счисления.
Шерлок берет каждое целое число от l до r, и выполняет над ним следующие операции:
- Выписывает все различные цифры, которые присутствуют в этом числе в шестнадцатеричной записи. Например, для 101416 он выпишет 1, 0, 4.
- Затем он складывает соответствующие степени двойки для каждой выписанной цифры. В примере выше sum = 21 + 20 + 24 = 1910.
- Затем Шерлок изменяет исходное число, выполняя операцию побитового xor над исходным числом и полученной суммой. Например,
 . Заметьте, что xor выполняется в двоичной системе счисления.
. Заметьте, что xor выполняется в двоичной системе счисления.
Другой пример: для числа 1e сумма равна sum = 21 + 214. Буквами a, b, c, d, e, f обозначаются шестнадцатеричные цифры 10, 11, 12, 13, 14, 15, соответственно.
Шерлок хочет найти количество чисел в диапазоне от l до r (включительно), которые уменьшатся после выполнения описанных четырех шагов. Он хочет, чтобы вы посчитали для него ответ для q различных вариантов l и r.
Первая строка содержит число q (1 ≤ q ≤ 10000).
Следующие q строк содержат по два числа l и r (0 ≤ l ≤ r < 1615) в шестнадцатеричной системе счисления.
Шестнадцатеричные числа записаны цифрами от 0 до 9 и/или буквами латинского алфавита a, b, c, d, e, f.
Шестнадцатеричные числа не содержат лишних лидирующих нулей.
Выведите q строк, строка i должна содержать ответ на i-й вопрос Шерлока (в десятеричной системе счисления).
1
1014 1014
1
2
1 1e
1 f
1
0
2
1 abc
d0e fe23
412
28464
Во втором тесте из примера:
1416 = 2010
sum = 21 + 24 = 18
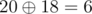
Это число уменьшается. Можно проверить, что это единственное число между 1 и 1e, которое уменьшается после выполнения операций.
| Название |
|---|




