You are given set of n points in 5-dimensional space. The points are labeled from 1 to n. No two points coincide.
We will call point a bad if there are different points b and c, not equal to a, from the given set such that angle between vectors 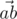 and
and 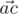 is acute (i.e. strictly less than
is acute (i.e. strictly less than 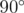 ). Otherwise, the point is called good.
). Otherwise, the point is called good.
The angle between vectors 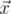 and
and 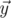 in 5-dimensional space is defined as
in 5-dimensional space is defined as 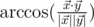 , where
, where 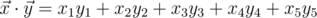 is the scalar product and
is the scalar product and 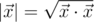 is length of
is length of 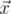 .
.
Given the list of points, print the indices of the good points in ascending order.
The first line of input contains a single integer n (1 ≤ n ≤ 103) — the number of points.
The next n lines of input contain five integers ai, bi, ci, di, ei (|ai|, |bi|, |ci|, |di|, |ei| ≤ 103) — the coordinates of the i-th point. All points are distinct.
First, print a single integer k — the number of good points.
Then, print k integers, each on their own line — the indices of the good points in ascending order.
6
0 0 0 0 0
1 0 0 0 0
0 1 0 0 0
0 0 1 0 0
0 0 0 1 0
0 0 0 0 1
1
1
3
0 0 1 2 0
0 0 9 2 0
0 0 5 9 0
0
In the first sample, the first point forms exactly a 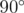 angle with all other pairs of points, so it is good.
angle with all other pairs of points, so it is good.
In the second sample, along the cd plane, we can see the points look as follows:
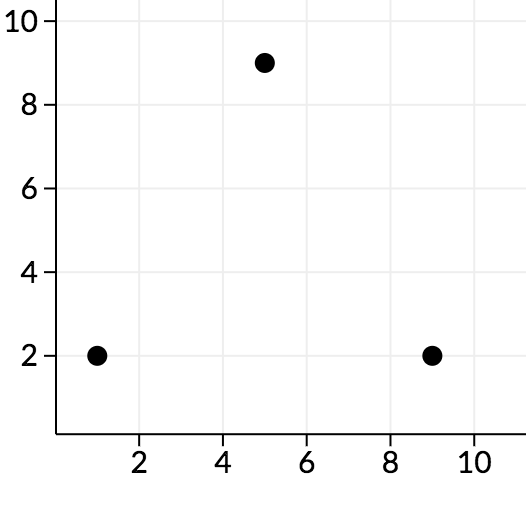
We can see that all angles here are acute, so no points are good.
| Name |
|---|




