Ivan is reading a book about tournaments. He knows that a tournament is an oriented graph with exactly one oriented edge between each pair of vertices. The score of a vertex is the number of edges going outside this vertex.
Yesterday Ivan learned Landau's criterion: there is tournament with scores d1 ≤ d2 ≤ ... ≤ dn if and only if 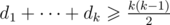 for all 1 ≤ k < n and
for all 1 ≤ k < n and 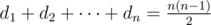 .
.
Now, Ivan wanna solve following problem: given a set of numbers S = {a1, a2, ..., am}, is there a tournament with given set of scores? I.e. is there tournament with sequence of scores d1, d2, ..., dn such that if we remove duplicates in scores, we obtain the required set {a1, a2, ..., am}?
Find a tournament with minimum possible number of vertices.
The first line contains a single integer m (1 ≤ m ≤ 31).
The next line contains m distinct integers a1, a2, ..., am (0 ≤ ai ≤ 30) — elements of the set S. It is guaranteed that all elements of the set are distinct.
If there are no such tournaments, print string "=(" (without quotes).
Otherwise, print an integer n — the number of vertices in the tournament.
Then print n lines with n characters — matrix of the tournament. The j-th element in the i-th row should be 1 if the edge between the i-th and the j-th vertices is oriented towards the j-th vertex, and 0 otherwise. The main diagonal should contain only zeros.
2
1 2
4
0011
1001
0100
0010
2
0 3
6
000111
100011
110001
011001
001101
000000
| Name |
|---|




