In this problem you will have to deal with a very special network.
The network consists of two parts: part A and part B. Each part consists of n vertices; i-th vertex of part A is denoted as Ai, and i-th vertex of part B is denoted as Bi.
For each index i (1 ≤ i < n) there is a directed edge from vertex Ai to vertex Ai + 1, and from Bi to Bi + 1, respectively. Capacities of these edges are given in the input. Also there might be several directed edges going from part A to part B (but never from B to A).
You have to calculate the maximum flow value from A1 to Bn in this network. Capacities of edges connecting Ai to Ai + 1 might sometimes change, and you also have to maintain the maximum flow value after these changes. Apart from that, the network is fixed (there are no changes in part B, no changes of edges going from A to B, and no edge insertions or deletions).
Take a look at the example and the notes to understand the structure of the network better.
The first line contains three integer numbers n, m and q (2 ≤ n, m ≤ 2·105, 0 ≤ q ≤ 2·105) — the number of vertices in each part, the number of edges going from A to B and the number of changes, respectively.
Then n - 1 lines follow, i-th line contains two integers xi and yi denoting that the edge from Ai to Ai + 1 has capacity xi and the edge from Bi to Bi + 1 has capacity yi (1 ≤ xi, yi ≤ 109).
Then m lines follow, describing the edges from A to B. Each line contains three integers x, y and z denoting an edge from Ax to By with capacity z (1 ≤ x, y ≤ n, 1 ≤ z ≤ 109). There might be multiple edges from Ax to By.
And then q lines follow, describing a sequence of changes to the network. i-th line contains two integers vi and wi, denoting that the capacity of the edge from Avi to Avi + 1 is set to wi (1 ≤ vi < n, 1 ≤ wi ≤ 109).
Firstly, print the maximum flow value in the original network. Then print q integers, i-th of them must be equal to the maximum flow value after i-th change.
4 3 2
1 2
3 4
5 6
2 2 7
1 4 8
4 3 9
1 100
2 100
9
14
14
This is the original network in the example:
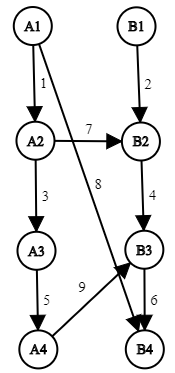
| Name |
|---|




