| VK Cup 2018 - Round 1 |
|---|
| Finished |
There is a number x initially written on a blackboard. You repeat the following action a fixed amount of times:
- take the number x currently written on a blackboard and erase it
- select an integer uniformly at random from the range [0, x] inclusive, and write it on the blackboard
Determine the distribution of final number given the distribution of initial number and the number of steps.
The first line contains two integers, N (1 ≤ N ≤ 105) — the maximum number written on the blackboard — and M (0 ≤ M ≤ 1018) — the number of steps to perform.
The second line contains N + 1 integers P0, P1, ..., PN (0 ≤ Pi < 998244353), where Pi describes the probability that the starting number is i. We can express this probability as irreducible fraction P / Q, then 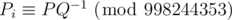 . It is guaranteed that the sum of all Pis equals 1 (modulo 998244353).
. It is guaranteed that the sum of all Pis equals 1 (modulo 998244353).
Output a single line of N + 1 integers, where Ri is the probability that the final number after M steps is i. It can be proven that the probability may always be expressed as an irreducible fraction P / Q. You are asked to output 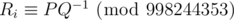 .
.
2 1
0 0 1
332748118 332748118 332748118
2 2
0 0 1
942786334 610038216 443664157
9 350
3 31 314 3141 31415 314159 3141592 31415926 314159265 649178508
822986014 12998613 84959018 728107923 939229297 935516344 27254497 413831286 583600448 442738326
In the first case, we start with number 2. After one step, it will be 0, 1 or 2 with probability 1/3 each.
In the second case, the number will remain 2 with probability 1/9. With probability 1/9 it stays 2 in the first round and changes to 1 in the next, and with probability 1/6 changes to 1 in the first round and stays in the second. In all other cases the final integer is 0.
| Name |
|---|




