A chip was placed on a field with coordinate system onto point (0, 0).
Every second the chip moves randomly. If the chip is currently at a point (x, y), after a second it moves to the point (x - 1, y) with probability p1, to the point (x, y - 1) with probability p2, to the point (x + 1, y) with probability p3 and to the point (x, y + 1) with probability p4. It's guaranteed that p1 + p2 + p3 + p4 = 1. The moves are independent.
Find out the expected time after which chip will move away from origin at a distance greater than R (i.e. 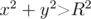 will be satisfied).
will be satisfied).
First line contains five integers R, a1, a2, a3 and a4 (0 ≤ R ≤ 50, 1 ≤ a1, a2, a3, a4 ≤ 1000).
Probabilities pi can be calculated using formula 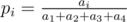 .
.
It can be shown that answer for this problem is always a rational number of form 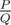 , where
, where 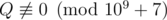 .
.
Print P·Q - 1 modulo 109 + 7.
0 1 1 1 1
1
1 1 1 1 1
666666674
1 1 2 1 2
538461545
In the first example initially the chip is located at a distance 0 from origin. In one second chip will move to distance 1 is some direction, so distance to origin will become 1.
Answers to the second and the third tests:  and
and  .
.
| Name |
|---|




