| Codeforces Round 479 (Div. 3) |
|---|
| Finished |
You are given an undirected graph consisting of $$$n$$$ vertices and $$$m$$$ edges. Your task is to find the number of connected components which are cycles.
Here are some definitions of graph theory.
An undirected graph consists of two sets: set of nodes (called vertices) and set of edges. Each edge connects a pair of vertices. All edges are bidirectional (i.e. if a vertex $$$a$$$ is connected with a vertex $$$b$$$, a vertex $$$b$$$ is also connected with a vertex $$$a$$$). An edge can't connect vertex with itself, there is at most one edge between a pair of vertices.
Two vertices $$$u$$$ and $$$v$$$ belong to the same connected component if and only if there is at least one path along edges connecting $$$u$$$ and $$$v$$$.
A connected component is a cycle if and only if its vertices can be reordered in such a way that:
- the first vertex is connected with the second vertex by an edge,
- the second vertex is connected with the third vertex by an edge,
- ...
- the last vertex is connected with the first vertex by an edge,
- all the described edges of a cycle are distinct.
A cycle doesn't contain any other edges except described above. By definition any cycle contains three or more vertices.
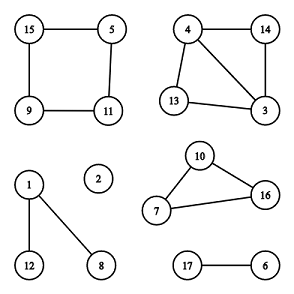 There are $$$6$$$ connected components, $$$2$$$ of them are cycles: $$$[7, 10, 16]$$$ and $$$[5, 11, 9, 15]$$$.
There are $$$6$$$ connected components, $$$2$$$ of them are cycles: $$$[7, 10, 16]$$$ and $$$[5, 11, 9, 15]$$$. The first line contains two integer numbers $$$n$$$ and $$$m$$$ ($$$1 \le n \le 2 \cdot 10^5$$$, $$$0 \le m \le 2 \cdot 10^5$$$) — number of vertices and edges.
The following $$$m$$$ lines contains edges: edge $$$i$$$ is given as a pair of vertices $$$v_i$$$, $$$u_i$$$ ($$$1 \le v_i, u_i \le n$$$, $$$u_i \ne v_i$$$). There is no multiple edges in the given graph, i.e. for each pair ($$$v_i, u_i$$$) there no other pairs ($$$v_i, u_i$$$) and ($$$u_i, v_i$$$) in the list of edges.
Print one integer — the number of connected components which are also cycles.
5 4
1 2
3 4
5 4
3 5
1
17 15
1 8
1 12
5 11
11 9
9 15
15 5
4 13
3 13
4 3
10 16
7 10
16 7
14 3
14 4
17 6
2
In the first example only component $$$[3, 4, 5]$$$ is also a cycle.
The illustration above corresponds to the second example.
| Name |
|---|




