| Codeforces Round 487 (Div. 2) |
|---|
| Закончено |
— Вода приходит и уходит, но не исчезает насовсем. Луна убывает и прибывает, но остается того же размера.
— Все приходящее. Все также вечно.
Канно не видит большого смысла в словах Мино, но, наверное, сейчас стоит просто насладиться легким бризом и ночным небом — неиссякаемыми дарами природы.
Глядя в звездное небо, Канно погружается в спокойный сон.
На плоскости отмечено множество $$$S$$$ из $$$n$$$ точек.
Канно начинает из некоторой точки плоскости $$$P$$$, которою может выбрать самостоятельно. $$$P$$$ не добавляется в $$$S$$$, если, конечно, изначально не принадлежит $$$S$$$. Затем следующая последовательность операций (вместе называющихся шагом) повторяется несколько раз:
- Выбирается прямая $$$l$$$ такая, что она проходит через как минимум две точки из $$$S$$$ и через текущую позицию Канно. Если таких прямых несколько, из них с равной вероятностью выбирается одна.
- Канно переходит в одну из точек из множества $$$S$$$ на прямой $$$l$$$. Точка назначения выбирается равновероятно из всех возможных, включая текущую позицию Канно, если она, конечно, принадлежит $$$S$$$.
Вам даны $$$q$$$ запросов, каждый из них состоит из двух целых чисел $$$(t_i, m_i)$$$. Для каждого запроса выведите максимально возможную вероятность для Канно оказаться в $$$t_i$$$-й точке множества $$$S$$$ после $$$m_i$$$ шагов при выборе оптимальной стартовой точки $$$P$$$. Обратите внимание, в соответствии с правилом 1 $$$P$$$ должна принадлежать как минимум одной прямой, которая проходит через две точки из $$$S$$$.
Первая строка содержит одно целое положительное число $$$n$$$ ($$$2 \leq n \leq 200$$$) — количество точек в $$$S$$$.
$$$i$$$-я из следующих $$$n$$$ строк содержит два целых числа $$$x_i$$$ и $$$y_i$$$ ($$$-10^4 \leq x_i, y_i \leq 10^4$$$) — координаты $$$i$$$-й точки множества $$$S$$$. Гарантируется, что для всех $$$1 \leq i \lt j \leq n$$$ выполняется $$$(x_i, y_i) \neq (x_j, y_j)$$$.
Следующая строка содержит одно целое число $$$q$$$ ($$$1 \leq q \leq 200$$$) — количество запросов.
Каждая из следующих $$$q$$$ строк содержит два целых числа $$$t$$$ и $$$m$$$ ($$$1 \leq t_i \leq n$$$, $$$1 \leq m_i \leq 10^4$$$) — номер точки финиша и количество шагов, соответственно.
Выведите $$$q$$$ строк, каждая из которых содержит одно вещественное число. $$$i$$$-е из этих чисел должно быть равно максимально возможной вероятности оказаться в точке $$$t_i$$$ после $$$m_i$$$ шагов при оптимальном выборе начальной точки $$$P$$$.
Ваш ответ будет считаться правильным, если каждое из чисел, выведенных вами, отличается от ответа жюри не более чем на $$$10^{-6}$$$.
Формально, пусть ваш ответ равен $$$a$$$, а ответ жюри равен $$$b$$$. Ваш ответ будет зачтен, если $$$|a - b| \le 10^{-6}$$$.
5
0 0
1 3
2 2
3 1
4 4
10
1 1
2 1
3 1
4 1
5 1
3 2
3 3
3 4
3 5
3 6
0.50000000000000000000
0.50000000000000000000
0.33333333333333331483
0.50000000000000000000
0.50000000000000000000
0.18518518518518517491
0.15226337448559670862
0.14494741655235482414
0.14332164812274550414
0.14296036624949901017
Точки множества $$$S$$$ и все возможные прямые $$$l$$$ показаны на рисунке ниже.
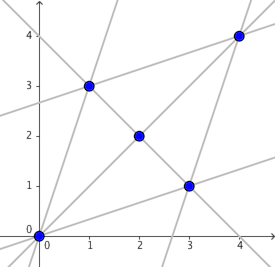
В первом примере если выбрать точку $$$P = (-1, -3)$$$, то в качестве $$$l$$$ будет обязательно выбрана точка $$$3x = y$$$, поэтому Канно переместится в $$$(0, 0)$$$ с вероятностью $$$\frac 1 2$$$.
В третьем запросе если выбрать точку $$$P = (2, 2)$$$, то $$$l$$$ будет выбрана с равной вероятностью между $$$x + y = 4$$$ и $$$x = y$$$. Тогда Канно переместится в остальные четыре точки с вероятностью $$$\frac 1 2 \cdot \frac 1 3 = \frac 1 6$$$ для каждой точки, и останется в $$$(2, 2)$$$ с вероятностью $$$\frac 1 3$$$.
| Название |
|---|




