| acmsguru |
|---|
| Закончено |
→ Теги задачи
Нет тегов
Нет прав на редактирование
Условие задачи было недавно изменено. Просмотреть изменения.
×
197. Nice Patterns Strike Back
time limit per test: 0.5 sec.
memory limit per test: 65536 KB
memory limit per test: 65536 KB
input: standard
output: standard
output: standard
You might have noticed that there is the new fashion among rich people to have their yards tiled with black and white tiles, forming a pattern. The company Broken Tiles is well known as the best tiling company in our region. It provides the widest choices of nice patterns to tile your yard with. The pattern is nice if there is no square of size 2 × 2, such that all tiles in it have the same color. So patterns on the figure 1 are nice, while patterns on the figure 2 are not.
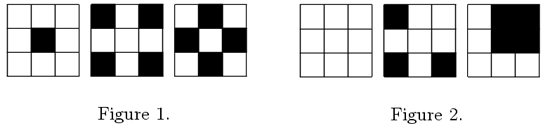
The president of the company wonders whether the variety of nice patterns he can provide to the clients is large enough. Thus he asks you to find out the number of nice patterns that can be used to tile the yard of size N × M. Now he is interested in the long term estimation, so he suggests N ≤ 10100. However, he does not like big numbers, so he asks you to find the answer modulo P.

The president of the company wonders whether the variety of nice patterns he can provide to the clients is large enough. Thus he asks you to find out the number of nice patterns that can be used to tile the yard of size N × M. Now he is interested in the long term estimation, so he suggests N ≤ 10100. However, he does not like big numbers, so he asks you to find the answer modulo P.
Input
The input file contains three integer numbers: N (1 ≤ N ≤ 10100), M (1 ≤ M ≤ 5) and P (1 ≤ P ≤ 10000).
Output
Write the number of nice patterns of size N × M modulo P to the output file.
Sample test(s)
Input
Test #1
2 2 5
Test #2
3 3 23
Output
Test #1
4
Test #2
0
| Author: | Andrew Stankevich |
| Resource: | Petrozavodsk Winter Trainings 2003 |
| Date: | 2003-02-06 |
Codeforces (c) Copyright 2010-2024 Михаил Мирзаянов
Соревнования по программированию 2.0
Время на сервере: 27.07.2024 03:35:57 (k2).
Десктопная версия, переключиться на мобильную.
При поддержке
Списки пользователей


| Название |
|---|




