| acmsguru |
|---|
| Finished |
→ Problem tags
No tags yet
No tag edit access
The problem statement has recently been changed. View the changes.
×
328. A Coloring Game
Time limit per test: 0.25 second(s)
Memory limit: 65536 kilobytes
Memory limit: 65536 kilobytes
input: standard
output: standard
output: standard
Two players play a graph coloring game. They make moves in turn, first player moves first. Initially they take some undirected graph. At each move, a player can color an uncolored vertex with either white or black color (each player can use any color, possibly different at different turns). It's not allowed to color two adjacent vertices with the same color. A player that can't move loses.
After playing this game for some time, they decided to study it. For a start, they've decided to study very simple kind of graph — a chain. A chain consists of N vertices, v1, v2,..., vN, and N-1 edges, connecting v1 with v2, v2 with v3,..., vN-1 with vN.
Given a position in this game, and assuming both players play optimally, who will win?
Input
The first line of input contains the integer N, 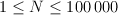 .
.The second line of input describes the current position. It contains N digits without spaces. ith digit describes the color of vertex vi: 0 — uncolored, 1 — black, 2 — white. No two vertices of the same color are adjacent.
Output
On the only line of output, print "FIRST" (without quotes) if the player moving first in that position wins the game, and "
SECOND" (without quotes) otherwise.
Example(s)
sample input | sample output |
5 00100 | SECOND |
sample input | sample output |
4 1020 | FIRST |
Codeforces (c) Copyright 2010-2024 Mike Mirzayanov
The only programming contests Web 2.0 platform
Server time: Apr/26/2024 20:51:55 (l1).
Desktop version, switch to mobile version.
Supported by
User lists


| Name |
|---|




