Пожалуйста, подпишитесь на официальный канал Codeforces в Telegram по ссылке https://t.me/codeforces_official.
×
| acmsguru |
|---|
| Закончено |
→ Теги задачи
Нет тегов
Нет прав на редактирование
Условие задачи было недавно изменено. Просмотреть изменения.
×
498. Coins
Time limit per test: 0.75 second(s)
Memory limit: 262144 kilobytes
Memory limit: 262144 kilobytes
input: standard
output: standard
output: standard
Andrew has just made a breakthrough in gambling: he has invented a way to make coins which have probability p of landing heads-up and 1 - p of landing tails-up when tossed, where p is some number between 0 and 1. He can't, however, control the number p itself, and creates coins with any p from 0 to 1 with equal probability. That is, the value of p is a random value uniformly distributed on
 . Andrew has generated two coins independently. One with probability p and another with probability q of landing heads-up. Random values p and q are both uniformly distributed on
. Andrew has generated two coins independently. One with probability p and another with probability q of landing heads-up. Random values p and q are both uniformly distributed on 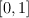 and are independent. Of course, neither Andrew nor we know the numbers p and q, we can only try to guess them using our observations. The observations are the following: the first coin was tossed n1 times, and m1 of them landed heads-up. The second coin was tossed n2 times, and m2 of them landed heads-up. Your task is to compute the probability that p < q.
and are independent. Of course, neither Andrew nor we know the numbers p and q, we can only try to guess them using our observations. The observations are the following: the first coin was tossed n1 times, and m1 of them landed heads-up. The second coin was tossed n2 times, and m2 of them landed heads-up. Your task is to compute the probability that p < q. Input
The first line of the input file contains one integer T (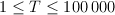 ) — the number of test cases to solve. Each of the following T lines contains 4 integers each: n1, m1, n2, m2. 1 ≤ n1, n2 ≤ 1000, 0 ≤ m1, m2 ≤ 50, 0 ≤ m1 ≤ n1, 0 ≤ m2 ≤ n2.
) — the number of test cases to solve. Each of the following T lines contains 4 integers each: n1, m1, n2, m2. 1 ≤ n1, n2 ≤ 1000, 0 ≤ m1, m2 ≤ 50, 0 ≤ m1 ≤ n1, 0 ≤ m2 ≤ n2. Output
For each test case output one line with a floating-point number, the probability of p < q. Your answer will be considered correct if it is within 10-4 of the right answer. Example(s)
sample input | sample output |
4 2 1 4 3 8 4 16 8 2 0 6 1 2 0 2 1 | 0.7142857142 0.5000000000 0.5333333333 0.8000000000 |
Codeforces (c) Copyright 2010-2024 Михаил Мирзаянов
Соревнования по программированию 2.0
Время на сервере: 21.07.2024 08:27:39 (j2).
Десктопная версия, переключиться на мобильную.
При поддержке
Списки пользователей


| Название |
|---|




