Please subscribe to the official Codeforces channel in Telegram via the link https://t.me/codeforces_official.
×
| acmsguru |
|---|
| Finished |
→ Problem tags
No tags yet
No tag edit access
The problem statement has recently been changed. View the changes.
×
545. Cut the rope, another rope and so on!
Time limit per test: 1 second(s)
Memory limit: 262144 kilobytes
Memory limit: 262144 kilobytes
input: standard
output: standard
output: standard
A game called "Cut the rope, another rope and so on!" is very popular in Berland. People all over the country just cut ropes on their bPads and bPhones over and over again.
The game is about sequentially cutting ropes with a small ball hanging on their ends. At the beginning of the game all ropes have one end attached to the top of the screen, that is, we can assume that the ends are located on the horizontal axis Ox. The other ends of the ropes are connected together and a small ball is attached to them. The ropes never shrink or stretch. At the beginning of the game the system is in a static state — some ropes are tight, some might be loose. In this game, the ball should be considered as a material point, that is, we assume that it is infinitely small.
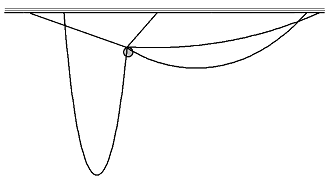
Let's suppose that at the beginning the ball is suspended on n ropes. A player cuts off n-1 uncut ropes, one after another. The ball may move in some way after some ropes are cut. The next cutting is made as soon as the ball becomes static after the previous cutting (the first cutting is made immediately). If the present cutting does not change the ball's position, then the next cutting is done immediately.
The physics in this game is a bit peculiar: educated people say that the motion of the ball is going in a perfectly viscous medium. This means that at any time the ball is moving so that it reduces the potential energy in the fastest way. For example, if the ball can fall straight down, it moves exactly this way. Note that the ball never swings, that is, its movement always moves it below its current position. You should assume that ropes have negligible masses compared with the mass of the ball.
Assuming that the ball always moves at the constant speed of 1 unit of length per unit of time, find the position of the ball at the given moments of time t1, t2,..., tm.
Input
The first input line contains two integers n and m (2 ≤ n ≤ 20; 1 ≤ m ≤ 1000) — the number of ropes and the number of ball position queries, correspondingly.The second line contains n integers x1, x2,..., xn (1 ≤ xi ≤ 200) — the coordinates of the ropes' attachment points on the horizontal axis.
The third line contains n integers l1, l2,..., ln (1 ≤ li ≤ 200), li is the length of the i-th rope. It is guaranteed that values x1, x2,..., xn and l1, l2,..., ln are such that the initial configuration really exists, that is, the lower ends of all ropes can be simultaneously tied to a ball. It is guaranteed that no two ropes have equal lengths and attached to the same point at the same time.
The fourth line describes the sequence of cuts, it contains n-1 distinct integers p1, p2,..., pn-1 (1 ≤ pj ≤ n), where pj is the index of the rope that is the j-th one to be cut.
The last input line contains m real numbers t1, t2,..., tm (0 ≤ tk ≤ 1000) — the moments of time for determining the ball's position. All ti are given with no more than three digits after the decimal point. The first rope is cut at time 0, each of the other ropes is cut at the moment the ball becomes stable after the cutting of the previous rope. If the current cutting doesn't change the ball's position, then the next rope is cut immediately. All values t1, t2,..., tm are distinct and are given in the increasing order.
Output
Print m lines, the k-th line must contain the coordinates of the ball at time tk. Consider all ropes attached to the Ox axis, and the Oy axis is directed upwards. Print the numbers with at least 5 digits after the decimal point. After the ball hangs on the last rope, it doesn't move anymore.Example(s)
sample input | sample output |
3 4 1 1 3 5 10 20 1 2 2.5 10 16 20 | 1.0000000000 -7.5000000000 1.0000000000 -15.0000000000 2.0972097000 -19.9796138520 3.0000000000 -20.0000000000 |
sample input | sample output |
3 7 2 22 19 12 12 10 2 1 0 0.18 0.19 4.39 6 7 9 | 12.0000000000 -6.6332495807 11.8993800085 -6.7824977292 11.8937244905 -6.7907448565 15.0867736994 -9.2025355158 16.6125973239 -9.7108345914 17.5939901889 -9.9006634329 19.0000000000 -10.0000000000 |
Codeforces (c) Copyright 2010-2024 Mike Mirzayanov
The only programming contests Web 2.0 platform
Server time: Jul/21/2024 08:28:44 (i1).
Desktop version, switch to mobile version.
Supported by
User lists


| Name |
|---|




