A. Will he Die?
Hint 1Due to symmetry, the answer of n m is equal to the answer of -n m, so work with the absolute value of n.
Hint 2We are looking for the probability of starting at position 0 and ending at n positions to the right, using m moves.
Hint 4So the answer will be the number of such strings that x - y = n where x is the number of 1's and y is the number of 0's, with some work on paper you can find that 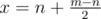 . Now the probability will be
. Now the probability will be  where mCx means m Choose x. You can handle the output format using the multiplicative inverse.
where mCx means m Choose x. You can handle the output format using the multiplicative inverse.
Hint 5If m - n is odd or negative then the answer is 0.
Vendetta. solution: https://ideone.com/N8WC9O
justHusam solution: https://ideone.com/oAPb42
Complexity: O(N) for pre-calculating factorials and 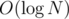 per test case for the multiplicative inverse.
per test case for the multiplicative inverse.
B. Ran and the Lock Code
Hint 1We need n numbers that sums up to n × a so that their average is equal to a.
Hint 2To choose the numbers to be the most distinct, we want to include as many smaller distinct number as possible so we will take numbers: 1, 2, 3 ..., x so that their summation is n × a, we can find x using Binary Search.
Why is it better to choose smaller numbers? because if we replace a small number with a bigger number, then we get closer to n × a thus less chances to use more distinct numbers.
Hint 3A problem arise when there is no summation from 1 to x that is equal to n × a, so we choose a summation less than n × a, and what's left will be equal to 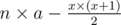 which will be distributed on n - x unused numbers (because we already used x numbers).
which will be distributed on n - x unused numbers (because we already used x numbers).
So at least we can give each of the n - x numbers a value of 1 since values must be positive, so 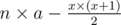 must be at least equal to n - x which will be our Binary Search condition which makes x a valid answer.
must be at least equal to n - x which will be our Binary Search condition which makes x a valid answer.
Vendetta. solution: https://ideone.com/VNyo8h
justHusam solution: https://ideone.com/KChjCF
Complexity: 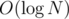 per test case.
per test case.
C. Professor Agasa Lab
Hint 1The answer is the number of possible values for a multiplied by the number of possible values for b.
Hint 2We can see that we can use any value for b from 1 to m - 1, thus m - 1 possible values for b, as for a, we can only use a value x that has a multiplicative inverse in respect to the module m which means x and m are co-primes, and the number of positive numbers co-primes with m less than m are calculated using the totient function. so the final answer is (m - 1) × Totient(m).
Vendetta. solution: https://ideone.com/Vz5u8p
Complexity: 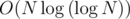 for pre-calculating totient and O(1) per test case.
for pre-calculating totient and O(1) per test case.
justHusam solution 1: https://ideone.com/yXLv7v
justHusam solution 2: https://ideone.com/s4EdLm
D. Help Conan
Hint 1Since the number of nodes are so low, you can work on all different subsets of nodes.
Hint 2One solution is a minimization Dynamic Programming, with state holding only a mask telling which nodes are already included in the spanning tree, and try to include any un-included node that can connect directly to one of the included nodes until all the important nodes are in the tree.
Hint 3Another slower solution is to find all the subsets of nodes that include all the important nodes, and do an MST for each of them and take the minimum.
Vendetta. solution: https://ideone.com/g6gcKd
Complexity: O(2N × N) per test case.
Complexity: O(2N × M) for the other slower solution per test case.
justHusam solution: https://ideone.com/uXfZUV (A bit different solution)
E. Rescue Haibara
Hint 1Minimize when the condition mentioned in the statement applies :)
Vendetta. solution: https://ideone.com/bF0axw
justHusam solution: https://ideone.com/LxK1PD
Complexity: O(N) per test case.
F. Median and Queries
Hint 1Since values are small, as well as the grid size, we can make a frequency array for every cell in a grid and make a 2D cumulative summation on every frequency array, this way we can get the frequency of a number in the sub-rectangle in O(1).
Hint 2For every query, loop over each number from 1 to 500 and find its frequency in that sub-rectangle, as we count the sum of the frequencies we know the median is at the element that makes the sum exceed half the size of the rectangle.
Hint 3The solution above gets AC, but to make the solution faster, we can do a cumulative summation on the frequency arrays so then we can binary search the point where the sum exceeds half the size of the sub-rectangle instead of looping over them.
Vendetta. solution: https://ideone.com/3EZ1SY
Complexity: per test case: O(N2 × Max(Ai)) for construction and O(Max(Ai)) per query.
justHusam solution: https://ideone.com/WEkeVH
Complexity: per test case: O(N2 × Max(Ai)) for construction and  per query.
per query.
G. Preparing for Exams
Hint 1Notice that abcd is a cyclic quadrilateral, which means its vertices all lie on a single circle.
Vendetta. solution: https://ideone.com/yKYgb9
justHusam solution 1: https://ideone.com/u8xofZ
justHusam solution 2: https://ideone.com/XNvyX9
Complexity: 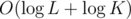 per test case since sqrt(x) complexity is
per test case since sqrt(x) complexity is  .
.
H. Genta Game
Hint 1Keep track of the number of different opposite characters, and at the end of each query add 1 to the answer if the number of different opposite characters is zero.
Vendetta. solution: https://ideone.com/C6X94O
justHusam solution: https://ideone.com/YYrF7f
Complexity: O(1) per query.
I. UEFA Champions League
Hint 1Read problem statement carefully to handle the cases where both teams have the same number of goals overall.
Vendetta. solution: https://ideone.com/NWtBvZ
justHusam solution: https://ideone.com/c7m35z
Complexity: O(1) per test case.
J. Gin Passwords
Hint 1You can solve this problem by brute forcing on the numbers from b down to a until you find a solution, this solution is valid and won't cause a Time Limit Exceeded.
Hint 2Why no TLE? because the biggest gap between any 2 consecutive 9 digits primes (half of the given number) is less than 320, so at most you will loop 320 times and find the second half of the number to be a prime and the GCD between a prime and any other number is 1, unless the other number is a multiple of that prime. but even if it is, the next prime number below that will work because if the first half is a multiple of both primes then it can't only be 9 digits (must be 18 digits if both primes are 9 digits). https://en.wikipedia.org/wiki/Prime_gap#Numerical_results
Vendetta. solution: https://ideone.com/bLV0UI
Complexity: O(Max(gn)) per test case where gn is the nth prime gap.
K. Conan and Scoreboard
Hint 1Show me your implementation powers :P
Vendetta. solution: https://ideone.com/0bLR7c
Complexity: 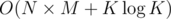 per test case.
per test case.
justHusam solution: https://ideone.com/aBKduB
Complexity: 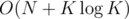 per test case.
per test case.
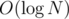 per test case for the multiplicative inverse.
per test case for the multiplicative inverse.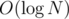 per test case.
per test case.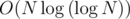 for pre-calculating totient and O(1) per test case.
for pre-calculating totient and O(1) per test case.  per query.
per query.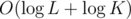 per test case since sqrt(x) complexity is
per test case since sqrt(x) complexity is  .
.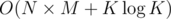 per test case.
per test case. 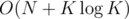 per test case.
per test case.


 and Left with probability
and Left with probability  as we have
as we have 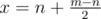 . Now the probability will be
. Now the probability will be  where
where 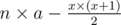 which will be distributed on
which will be distributed on 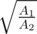 , from which we can find
, from which we can find 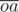 and
and 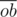 then
then 

