Firstly, huge thanks to [user:Noam527,2020-04-07] for guiding me to this solution by providing his output for `N = 255`. This probably wouldn't have been possible without his help.↵
↵
As some of you may know, getting 100 points for [IOI 2003 Reverse](https://contest.yandex.ru/ioi/contest/558/problems/C/) is [pretty](https://codeforces.com/blog/entry/66014?#comment-499829) [difficult](https://contest.yandex.ru/ioi/contest/558/standings/). The [editorial](https://github.com/mostafa-saad/MyCompetitiveProgramming/blob/master/Olympiad/IOI/official/2003/reverse.pdf) only explains an 88-point solution and there seemed to be no publicly available code online that scored 100 points when I solved it.↵
↵
This blog post serves as a tutorial for those who are stuck with 88 points (or less) but who would like 100 points (to fill in that last yellow cell on OIChecklist or just to flex).↵
↵
### 88-point solution↵
↵
I'll just quote the editorial for this solution.↵
↵
> Consider the case of trying to solve each input with only one `S`-operation. Clearly, register 1 might as well as be initialized to `N`. The register 2 can be `N - 2`. After printing out `N`, one `S`-operation turns register 1 to `N - 1`. Register 3 can be `N - 5`. After printing `N - 2`, `S 3 1` makes register 1 `N - 4`. After printing out `N - 2`, `S 1 2` turns register 2 into `N - 3`, the next value to output. Continuing this through all the registers, 44 is the largest value of `N` which can be solved in only one `S`-operation. This algorithm scores 90% of the points if extended to dealing with multiple operations.↵
↵
<spoiler summary="My code for 88 points">```cpp↵
#include <bits/stdc++.h>↵
#define FOR(i, x, y) for (int i = x; i < y; i++)↵
typedef long long ll;↵
using namespace std;↵
↵
int n, k, reg[9];↵
int lim[8]{8, 44, 80, 116, 152, 188, 224, 260};↵
↵
void INIT(int V, int P) {↵
printf("%d", V);↵
if (P == 8) printf("\n");↵
else printf(" ");↵
reg[P] = V;↵
}↵
↵
void ADD(int A, int B) {↵
reg[B] = reg[A] + 1;↵
printf("S %d %d\n", A + 1, B + 1);↵
}↵
↵
int FIND(int V) { return find(reg, reg + 9, V) - reg; }↵
↵
void PRINT(int P) { printf("P %d\n", P + 1); }↵
↵
int main() {↵
scanf("%d %d", &k, &n);↵
printf("FILE reverse %d\n", k);↵
↵
int mx = lower_bound(lim, lim + 8, n) - lim;↵
↵
int c = n;↵
FOR(i, 0, 9) {↵
INIT(max(0, c), i);↵
c -= mx * i + mx + 1;↵
}↵
↵
int nxt = 1, curr = -1, rising = 1;↵
n++;↵
while (n--) {↵
int pos = FIND(n);↵
if (pos == 9) {↵
FOR(i, 1, mx + 1) {↵
pos = FIND(n - i);↵
if (pos != 9) {↵
ADD(pos, curr);↵
FOR(j, 1, i) ADD(curr, curr);↵
PRINT(curr);↵
break;↵
}↵
}↵
} else {↵
if (pos == rising && nxt != 8) rising = ++nxt;↵
if (~curr && mx && reg[rising] + mx < n) {↵
ADD(rising, curr);↵
FOR(i, 1, mx) ADD(curr, curr);↵
rising = curr;↵
}↵
PRINT(pos);↵
curr = pos;↵
}↵
}↵
return 0;↵
}↵
```↵
</spoiler>↵
↵
The code for 88 points is pretty clean and elegant. Most people would stop here. However, if you <s>hate yourself</s> want a challenge, then you'd probably try to get 100 points.↵
↵
### 100-point solution↵
↵
The 100-point solution is a relatively simple extension of the 88-point solution.↵
↵
With the 88-point solution, the only test cases whereyouwe won't get AC are probably the cases with `N = 97` (`MAX_S = 2`) or `N > 188` (`MAX_S = 4`).↵
↵
Consider the output of the 88-point code for `N = 97` (the optimal `MAX_S` is 2; the `MAX_S` here is 3):↵
↵
```↵
97 93 86 76 63 47 28 6 0↵
P 1↵
S 2 1↵
S 1 1↵
S 1 1↵
P 1↵
S 2 1↵
S 1 1↵
P 1↵
S 2 1↵
P 1↵
S 3 1↵
S 1 1↵
S 1 1↵
P 2↵
S 1 2↵
S 2 2↵
S 2 2↵
P 2↵
S 1 2↵
S 2 2↵
P 2↵
S 1 2↵
P 2↵
etc.↵
```↵
↵
Notice anything inefficient?↵
↵
That's right — we can use up to 3 consecutive `S`-operations but there are many places where we only use 1 or 2 consecutive `S`-operations. We are effectively wasting `S`-operations.↵
↵
Moreover, we can increment any of the 9 values but for each block of consecutive `S`-operations, we only increase 1.↵
↵
Here are the first few lines of output for the same case but with the 100-points code:↵
↵
```↵
97 94 89 81 70 56 39 19 0↵
P 1↵
S 2 1↵
S 1 1↵
P 1↵
S 2 1↵
P 1↵
S 3 1↵
S 1 1↵
P 2↵
S 1 2↵
S 2 2↵
P 2↵
S 1 2↵
P 2↵
```↵
↵
This is quite similar to the previous output (albeit with only 2 consecutive `S`-operations instead of 3), but it's the next few lines we should be interested in:↵
↵
```↵
S 4 2↵
S 2 2↵
P 1↵
S 3 1↵
S 2 2↵
P 1↵
```↵
↵
Notice how in the 4th and 5th lines, instead of only increasing the value from 1 register, we increase the value from 2 separate registers.↵
↵
This means that we can waste fewer `S`-operations! Whereas the 88-point solution would alternate between 1 `S`-operation and 2 `S`-operations, the 100-point solution would have sections with only 2 consecutive `S`-operations, like↵
↵
```↵
S 2 1↵
S 3 3↵
P 1↵
S 4 1↵
S 1 1↵
P 2↵
S 3 2↵
S 2 2↵
P 1↵
S 4 1↵
S 2 2↵
P 1↵
S 2 1↵
S 1 1↵
P 4↵
```↵
↵
If we continue this pattern, we notice 2 things:↵
↵
- The consecutive differences between the starting values of the registers (excluding the first) for an arithmetic sequence of the form $3N + 2$↵
- There are 2 types of "cycles" — type 1 is when we "fill in" wasted `S`-operations (like above) and type 2 is when we simply follow the strategy of the 88-point solution. We start on a type 2 cycle and whenever we need to print a value that is already present in some register, we switch to the other cycle.↵
↵
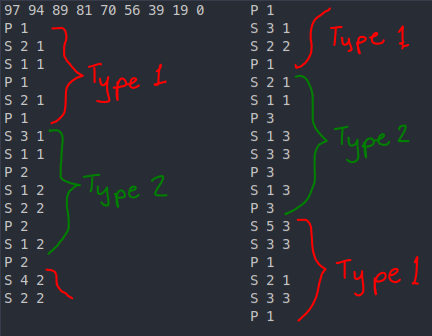↵
↵
Using this new strategy, we can use only 2 consecutive `S`-operations for up to `N = 101`!↵
↵
It turns out that if we use the arithmetic sequence $9N$ instead of $3N + 2$, this strategy also works for 4 consecutive `S`-operations for up to `N = 257`.↵
↵
I found the implementation for this to be quite tricky and I had to use the 88-point code for `MAX_S != 2` and `MAX_S != 4`.↵
↵
<spoiler summary="My (somewhat messy) code for 100 points">```cpp↵
#include <bits/stdc++.h>↵
#define FOR(i, x, y) for (int i = x; i < y; i++)↵
using namespace std;↵
↵
int n, k, reg[9];↵
int lim[5]{8, 44, 97, 116, 257};↵
↵
void INIT(int V, int P) {↵
printf("%d", V);↵
if (P == 8) printf("\n");↵
else printf(" ");↵
reg[P] = V;↵
}↵
↵
void ADD(int A, int B) {↵
printf("S %d %d\n", A + 1, B + 1);↵
reg[B] = reg[A] + 1;↵
}↵
↵
int FIND(int V) { return find(reg, reg + 9, V) - reg; }↵
↵
void PRINT(int P) { printf("P %d\n", P + 1); }↵
↵
int main() {↵
scanf("%d %d", &k, &n);↵
printf("FILE reverse %d\n", k);↵
↵
int mx = lower_bound(lim, lim + 8, n) - lim;↵
↵
if (mx == 4 || mx == 2) {↵
int c = n, diff1 = (mx == 2 ? 3 : 9), diff2 = (mx == 2 ? 2 : 0);↵
INIT(c, 0);↵
INIT(c - mx - 1, 1);↵
c -= mx + 1;↵
FOR(i, 1, 8) {↵
c -= i * diff1 + diff2;↵
INIT(max(c, 0), i + 1);↵
}↵
↵
int nxt = 2, curr, rising = -1;↵
queue<int> to_rise;↵
bool twice = true;↵
↵
n++;↵
while (n--) {↵
curr = FIND(n);↵
PRINT(curr);↵
if (!n) break;↵
↵
int pos = FIND(n - 1);↵
if (pos == 9) {↵
FOR(i, 1, mx + 1) {↵
pos = FIND(n - 1 - i);↵
if (pos != 9) {↵
ADD(pos, curr);↵
for (int j = 1; j < i && reg[curr] < n - 1; j++) ADD(curr, curr);↵
↵
if ((i != mx - 1 || mx == 2) && twice && rising > -1 && rising < 9 && rising != pos)↵
for (int j = i; j < mx && reg[rising] < n - 1; j++) ADD(rising, rising);↵
↵
break;↵
}↵
}↵
} else {↵
twice = !twice;↵
if (twice && nxt != 9) {↵
if (!to_rise.size()) {↵
nxt++;↵
FOR(i, 0, nxt - 2) to_rise.push(reg[nxt] + i * diff1);↵
}↵
rising = FIND(to_rise.front());↵
to_rise.pop();↵
} else {↵
FOR(j, 2, 2 * mx + 3) {↵
rising = FIND(n - j);↵
if (rising != 9) break;↵
}↵
}↵
↵
if (rising != 9) {↵
ADD(rising, curr);↵
for (int i = 1; i < mx && reg[curr] < n - 2; i++) ADD(curr, curr);↵
rising = curr;↵
}↵
}↵
}↵
} else {↵
int c = n;↵
FOR(i, 0, 9) {↵
INIT(max(0, c), i);↵
c -= mx * i + mx + 1;↵
}↵
↵
int nxt = 1, curr = -1, rising = 1;↵
n++;↵
while (n--) {↵
int pos = FIND(n);↵
if (pos == 9) {↵
FOR(i, 1, mx + 1) {↵
pos = FIND(n - i);↵
if (pos != 9) {↵
ADD(pos, curr);↵
FOR(j, 1, i) ADD(curr, curr);↵
PRINT(curr);↵
break;↵
}↵
}↵
} else {↵
if (pos == rising && nxt != 8) rising = ++nxt;↵
if (~curr && mx && reg[rising] + mx < n) {↵
ADD(rising, curr);↵
FOR(i, 1, mx) ADD(curr, curr);↵
rising = curr;↵
}↵
PRINT(pos);↵
curr = pos;↵
}↵
}↵
}↵
return 0;↵
}↵
```↵
</spoiler>↵
↵
Unfortunately, when I used $6N + 1$ for the `MAX_S = 3` case, it got RTE on some cases. This didn't matter though since the test data was weak enough for a sub-optimal `MAX_S = 3` solution to pass. However, I believe it should work for up to `N = 179`.↵
↵
If anyone can improve my code or make it more general, please let me know in the comments. Additionally, if anything isn't clear, please let me know so I can try to fix it.
↵
As some of you may know, getting 100 points for [IOI 2003 Reverse](https://contest.yandex.ru/ioi/contest/558/problems/C/) is [pretty](https://codeforces.com/blog/entry/66014?#comment-499829) [difficult](https://contest.yandex.ru/ioi/contest/558/standings/). The [editorial](https://github.com/mostafa-saad/MyCompetitiveProgramming/blob/master/Olympiad/IOI/official/2003/reverse.pdf) only explains an 88-point solution and there seemed to be no publicly available code online that scored 100 points when I solved it.↵
↵
This blog post serves as a tutorial for those who are stuck with 88 points (or less) but who would like 100 points (to fill in that last yellow cell on OIChecklist or just to flex).↵
↵
### 88-point solution↵
↵
I'll just quote the editorial for this
↵
> Consider the case of trying to solve each input with only one `S`-operation. Clearly, register 1 might as well as be initialized to `N`. The register 2 can be `N - 2`. After printing out `N`, one `S`-operation turns register 1 to `N - 1`. Register 3 can be `N - 5`. After printing `N - 2`, `S 3 1` makes register 1 `N - 4`. After printing out `N - 2`, `S 1 2` turns register 2 into `N - 3`, the next value to output. Continuing this through all the registers, 44 is the largest value of `N` which can be solved in only one `S`-operation. This algorithm scores 90% of the points if extended to dealing with multiple operations.↵
↵
<spoiler summary="My code for 88 points">```cpp↵
#include <bits/stdc++.h>↵
#define FOR(i, x, y) for (int i = x; i < y; i++)↵
typedef long long ll;↵
using namespace std;↵
↵
int n, k, reg[9];↵
int lim[8]{8, 44, 80, 116, 152, 188, 224, 260};↵
↵
void INIT(int V, int P) {↵
printf("%d", V);↵
if (P == 8) printf("\n");↵
else printf(" ");↵
reg[P] = V;↵
}↵
↵
void ADD(int A, int B) {↵
reg[B] = reg[A] + 1;↵
printf("S %d %d\n", A + 1, B + 1);↵
}↵
↵
int FIND(int V) { return find(reg, reg + 9, V) - reg; }↵
↵
void PRINT(int P) { printf("P %d\n", P + 1); }↵
↵
int main() {↵
scanf("%d %d", &k, &n);↵
printf("FILE reverse %d\n", k);↵
↵
int mx = lower_bound(lim, lim + 8, n) - lim;↵
↵
int c = n;↵
FOR(i, 0, 9) {↵
INIT(max(0, c), i);↵
c -= mx * i + mx + 1;↵
}↵
↵
int nxt = 1, curr = -1, rising = 1;↵
n++;↵
while (n--) {↵
int pos = FIND(n);↵
if (pos == 9) {↵
FOR(i, 1, mx + 1) {↵
pos = FIND(n - i);↵
if (pos != 9) {↵
ADD(pos, curr);↵
FOR(j, 1, i) ADD(curr, curr);↵
PRINT(curr);↵
break;↵
}↵
}↵
} else {↵
if (pos == rising && nxt != 8) rising = ++nxt;↵
if (~curr && mx && reg[rising] + mx < n) {↵
ADD(rising, curr);↵
FOR(i, 1, mx) ADD(curr, curr);↵
rising = curr;↵
}↵
PRINT(pos);↵
curr = pos;↵
}↵
}↵
return 0;↵
}↵
```↵
</spoiler>↵
↵
The code for 88 points is pretty clean and elegant. Most people would stop here. However, if you <s>hate yourself</s> want a challenge, then you'd probably try to get 100 points.↵
↵
### 100-point solution↵
↵
The 100-point solution is a relatively simple extension of the 88-point solution.↵
↵
With the 88-point solution, the only test cases where
↵
Consider the output of the 88-point code for `N = 97` (the optimal `MAX_S` is 2; the `MAX_S` here is 3):↵
↵
```↵
97 93 86 76 63 47 28 6 0↵
P 1↵
S 2 1↵
S 1 1↵
S 1 1↵
P 1↵
S 2 1↵
S 1 1↵
P 1↵
S 2 1↵
P 1↵
S 3 1↵
S 1 1↵
S 1 1↵
P 2↵
S 1 2↵
S 2 2↵
S 2 2↵
P 2↵
S 1 2↵
S 2 2↵
P 2↵
S 1 2↵
P 2↵
etc.↵
```↵
↵
Notice anything inefficient?↵
↵
That's right — we can use up to 3 consecutive `S`-operations but there are many places where we only use 1 or 2 consecutive `S`-operations. We are effectively wasting `S`-operations.↵
↵
Moreover, we can increment any of the 9 values but for each block of consecutive `S`-operations, we only increase 1.↵
↵
Here are the first few lines of output for the same case but with the 100-points code:↵
↵
```↵
97 94 89 81 70 56 39 19 0↵
P 1↵
S 2 1↵
S 1 1↵
P 1↵
S 2 1↵
P 1↵
S 3 1↵
S 1 1↵
P 2↵
S 1 2↵
S 2 2↵
P 2↵
S 1 2↵
P 2↵
```↵
↵
This is quite similar to the previous output (albeit with only 2 consecutive `S`-operations instead of 3), but it's the next few lines we should be interested in:↵
↵
```↵
S 4 2↵
S 2 2↵
P 1↵
S 3 1↵
S 2 2↵
P 1↵
```↵
↵
Notice how in the 4th and 5th lines, instead of only increasing the value from 1 register, we increase the value from 2 separate registers.↵
↵
This means that we can waste fewer `S`-operations! Whereas the 88-point solution would alternate between 1 `S`-operation and 2 `S`-operations, the 100-point solution would have sections with only 2 consecutive `S`-operations, like↵
↵
```↵
S 2 1↵
S 3 3↵
P 1↵
S 4 1↵
S 1 1↵
P 2↵
S 3 2↵
S 2 2↵
P 1↵
S 4 1↵
S 2 2↵
P 1↵
S 2 1↵
S 1 1↵
P 4↵
```↵
↵
If we continue this pattern, we notice 2 things:↵
↵
- The consecutive differences between the starting values of the registers (excluding the first) for an arithmetic sequence of the form $3N + 2$↵
- There are 2 types of "cycles" — type 1 is when we "fill in" wasted `S`-operations (like above) and type 2 is when we simply follow the strategy of the 88-point solution. We start on a type 2 cycle and whenever we need to print a value that is already present in some register, we switch to the other cycle.↵
↵
↵
↵
Using this new strategy, we can use only 2 consecutive `S`-operations for up to `N = 101`!↵
↵
It turns out that if we use the arithmetic sequence $9N$ instead of $3N + 2$, this strategy also works for 4 consecutive `S`-operations for up to `N = 257`.↵
↵
I found the implementation for this to be quite tricky and I had to use the 88-point code for `MAX_S != 2` and `MAX_S != 4`.↵
↵
<spoiler summary="My (somewhat messy) code for 100 points">```cpp↵
#include <bits/stdc++.h>↵
#define FOR(i, x, y) for (int i = x; i < y; i++)↵
using namespace std;↵
↵
int n, k, reg[9];↵
int lim[5]{8, 44, 97, 116, 257};↵
↵
void INIT(int V, int P) {↵
printf("%d", V);↵
if (P == 8) printf("\n");↵
else printf(" ");↵
reg[P] = V;↵
}↵
↵
void ADD(int A, int B) {↵
printf("S %d %d\n", A + 1, B + 1);↵
reg[B] = reg[A] + 1;↵
}↵
↵
int FIND(int V) { return find(reg, reg + 9, V) - reg; }↵
↵
void PRINT(int P) { printf("P %d\n", P + 1); }↵
↵
int main() {↵
scanf("%d %d", &k, &n);↵
printf("FILE reverse %d\n", k);↵
↵
int mx = lower_bound(lim, lim + 8, n) - lim;↵
↵
if (mx == 4 || mx == 2) {↵
int c = n, diff1 = (mx == 2 ? 3 : 9), diff2 = (mx == 2 ? 2 : 0);↵
INIT(c, 0);↵
INIT(c - mx - 1, 1);↵
c -= mx + 1;↵
FOR(i, 1, 8) {↵
c -= i * diff1 + diff2;↵
INIT(max(c, 0), i + 1);↵
}↵
↵
int nxt = 2, curr, rising = -1;↵
queue<int> to_rise;↵
bool twice = true;↵
↵
n++;↵
while (n--) {↵
curr = FIND(n);↵
PRINT(curr);↵
if (!n) break;↵
↵
int pos = FIND(n - 1);↵
if (pos == 9) {↵
FOR(i, 1, mx + 1) {↵
pos = FIND(n - 1 - i);↵
if (pos != 9) {↵
ADD(pos, curr);↵
for (int j = 1; j < i && reg[curr] < n - 1; j++) ADD(curr, curr);↵
↵
if ((i != mx - 1 || mx == 2) && twice && rising > -1 && rising < 9 && rising != pos)↵
for (int j = i; j < mx && reg[rising] < n - 1; j++) ADD(rising, rising);↵
↵
break;↵
}↵
}↵
} else {↵
twice = !twice;↵
if (twice && nxt != 9) {↵
if (!to_rise.size()) {↵
nxt++;↵
FOR(i, 0, nxt - 2) to_rise.push(reg[nxt] + i * diff1);↵
}↵
rising = FIND(to_rise.front());↵
to_rise.pop();↵
} else {↵
FOR(j, 2, 2 * mx + 3) {↵
rising = FIND(n - j);↵
if (rising != 9) break;↵
}↵
}↵
↵
if (rising != 9) {↵
ADD(rising, curr);↵
for (int i = 1; i < mx && reg[curr] < n - 2; i++) ADD(curr, curr);↵
rising = curr;↵
}↵
}↵
}↵
} else {↵
int c = n;↵
FOR(i, 0, 9) {↵
INIT(max(0, c), i);↵
c -= mx * i + mx + 1;↵
}↵
↵
int nxt = 1, curr = -1, rising = 1;↵
n++;↵
while (n--) {↵
int pos = FIND(n);↵
if (pos == 9) {↵
FOR(i, 1, mx + 1) {↵
pos = FIND(n - i);↵
if (pos != 9) {↵
ADD(pos, curr);↵
FOR(j, 1, i) ADD(curr, curr);↵
PRINT(curr);↵
break;↵
}↵
}↵
} else {↵
if (pos == rising && nxt != 8) rising = ++nxt;↵
if (~curr && mx && reg[rising] + mx < n) {↵
ADD(rising, curr);↵
FOR(i, 1, mx) ADD(curr, curr);↵
rising = curr;↵
}↵
PRINT(pos);↵
curr = pos;↵
}↵
}↵
}↵
return 0;↵
}↵
```↵
</spoiler>↵
↵
Unfortunately, when I used $6N + 1$ for the `MAX_S = 3` case, it got RTE on some cases. This didn't matter though since the test data was weak enough for a sub-optimal `MAX_S = 3` solution to pass. However, I believe it should work for up to `N = 179`.↵
↵
If anyone can improve my code or make it more general, please let me know in the comments. Additionally, if anything isn't clear, please let me know so I can try to fix it.





