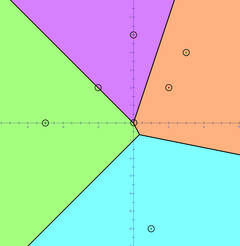
Figure: Voronoi Diagram of size 4.
In the 2-dimensional Cartesian coordinate system, we define the Voronoi Diagram of a non-empty set of points $$$S$$$, as a diagram that divides the plane by the criteria "which point in the set $$$S$$$ is closest in this location?". More precisely, the Voronoi diagram of a given non-empty point set $$$\{P_1, P_2, \cdots, P_n\}$$$ is a collection of regions: A point $$$K$$$ is included in region $$$i$$$ if and only if $$$d(P_i, K) \le d(P_j, K)$$$ holds for all $$$1 \le j \le n$$$, where $$$d(X, Y)$$$ denotes the Euclidean distance between point $$$X$$$ and $$$Y$$$.
For example, in the picture above, every location over the plane is colored by the closest point with such location. The points which belongs to a single region is colored by a light color indicating a region, and the points which belongs to more than one region forms lines and points colored black.
There is an algorithm which computes the Voronoi Diagram in $$$O(n \log(n))$$$, but it is infamous to be very complicated and hard. In fact, we are lenient problem setters, so we set $$$n \leq 2000$$$, which means you can solve this task with slower Voronoi Diagram algorithms!
In this task, you should solve the point query problem in Voronoi diagram: in the Voronoi diagram constructed with the set of points $$$\{P_1, P_2, \cdots, P_n\}$$$, you should determine which region(s) the point belongs in. More precisely, you will be given $$$q$$$ queries of points. For each query point, you should determine the following:
- If it's not included in any region, output NONE.
- If it's included in exactly one region, output REGION X, where X is the index of such region.
- If it's included in exactly two regions, output LINE X Y, where X and Y (X $$$<$$$ Y) are the indices of such two regions.
- If it's included in three or more regions, output POINT.
In the first line, the number of points consisting Voronoi diagram $$$n$$$, and the number of queries $$$q$$$ are given. ($$$3 \le n \le 2\ 000, 1 \le q \le 250\ 000$$$)
In the $$$i$$$th line of next $$$n$$$ lines, two integers indicating $$$x$$$ and $$$y$$$ co-ordinate of $$$P_i$$$ are given. These are the points consisting the Voronoi diagram. All $$$n$$$ points are distinct. ($$$|x|, |y| \le 10^4$$$)
In the $$$j$$$th line of next $$$q$$$ lines, two integers indicating $$$x$$$ and $$$y$$$ co-ordinate of $$$Q_j$$$ are given. For each point $$$Q_j$$$, you should determine in which region(s) the given point belongs to. ($$$|x|, |y| \le 10^4$$$)
Output consists of $$$q$$$ lines. In the $$$j$$$th line, you should print one of following:
- If $$$Q_j$$$ is not included in any region, output NONE.
- If $$$Q_j$$$ is included in exactly one region, output REGION X, where X is the index of such region.
- If $$$Q_j$$$ is included in exactly two regions, output LINE X Y, where X and Y (X $$$<$$$ Y) are the indices of such two regions.
- If $$$Q_j$$$ is included in three or more regions, output POINT.
4 3
-5 0
0 5
3 4
1 -6
-2 2
0 0
2 2
LINE 1 2
POINT
REGION 3
Example is illustrated as diagram above.
| Name |
|---|




