Gerald is positioned in an old castle which consists of n halls connected with n - 1 corridors. It is exactly one way to go from any hall to any other one. Thus, the graph is a tree. Initially, at the moment of time 0, Gerald is positioned in hall 1. Besides, some other hall of the castle contains the treasure Gerald is looking for. The treasure's position is not known; it can equiprobably be in any of other n - 1 halls. Gerald can only find out where the treasure is when he enters the hall with the treasure. That very moment Gerald sees the treasure and the moment is regarded is the moment of achieving his goal.
The corridors have different lengths. At that, the corridors are considered long and the halls are considered small and well lit. Thus, it is possible not to take the time Gerald spends in the halls into consideration. The castle is very old, that's why a corridor collapses at the moment when somebody visits it two times, no matter in which direction.
Gerald can move around the castle using the corridors; he will go until he finds the treasure. Naturally, Gerald wants to find it as quickly as possible. In other words, he wants to act in a manner that would make the average time of finding the treasure as small as possible. Each corridor can be used no more than two times. That's why Gerald chooses the strategy in such a way, so he can visit every hall for sure.
More formally, if the treasure is located in the second hall, then Gerald will find it the moment he enters the second hall for the first time — let it be moment t2. If the treasure is in the third hall, then Gerald will find it the moment he enters the third hall for the first time. Let it be the moment of time t3. And so on. Thus, the average time of finding the treasure will be equal to 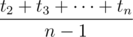 .
.
The first line contains the only integer n (2 ≤ n ≤ 105) — the number of halls in the castle. Next n - 1 lines each contain three integers. The i-th line contains numbers ai, bi and ti (1 ≤ ai, bi ≤ n, ai ≠ bi, 1 ≤ ti ≤ 1000) — the numbers of halls connected with the i-th corridor and the time needed to go along the corridor. Initially Gerald is in the hall number 1. It is guaranteed that one can get from any hall to any other one using corridors.
Print the only real number: the sought expectation of time needed to find the treasure. The answer should differ from the right one in no less than 10 - 6.
2
1 2 1
1.0
4
1 3 2
4 2 1
3 2 3
4.333333333333334
5
1 2 1
1 3 1
1 4 1
1 5 1
4.0
In the first test the castle only has two halls which means that the treasure is located in the second hall. Gerald will only need one minute to go to the second hall from the first one.
In the second test Gerald can only go from the first hall to the third one. He can get from the third room to the first one or to the second one, but he has already visited the first hall and can get nowhere from there. Thus, he needs to go to the second hall. He should go to hall 4 from there, because all other halls have already been visited. If the treasure is located in the third hall, Gerald will find it in a minute, if the treasure is located in the second hall, Gerald finds it in two minutes, if the treasure is in the fourth hall, Gerald will find it in three minutes. The average time makes 2 minutes.
In the third test Gerald needs to visit 4 halls: the second, third, fourth and fifth ones. All of them are only reachable from the first hall. Thus, he needs to go to those 4 halls one by one and return. Gerald will enter the first of those halls in a minute, in the second one — in three minutes, in the third one - in 5 minutes, in the fourth one - in 7 minutes. The average time is 4 minutes.
| Name |
|---|




