Let's denote a $$$k$$$-step ladder as the following structure: exactly $$$k + 2$$$ wooden planks, of which
- two planks of length at least $$$k+1$$$ — the base of the ladder;
- $$$k$$$ planks of length at least $$$1$$$ — the steps of the ladder;
Note that neither the base planks, nor the steps planks are required to be equal.
For example, ladders $$$1$$$ and $$$3$$$ are correct $$$2$$$-step ladders and ladder $$$2$$$ is a correct $$$1$$$-step ladder. On the first picture the lengths of planks are $$$[3, 3]$$$ for the base and $$$[1]$$$ for the step. On the second picture lengths are $$$[3, 3]$$$ for the base and $$$[2]$$$ for the step. On the third picture lengths are $$$[3, 4]$$$ for the base and $$$[2, 3]$$$ for the steps.
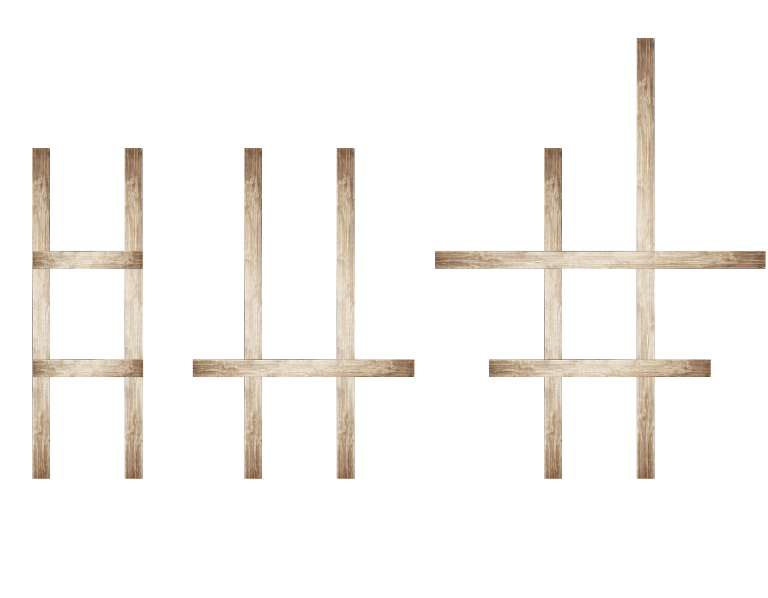
You have $$$n$$$ planks. The length of the $$$i$$$-th planks is $$$a_i$$$. You don't have a saw, so you can't cut the planks you have. Though you have a hammer and nails, so you can assemble the improvised "ladder" from the planks.
The question is: what is the maximum number $$$k$$$ such that you can choose some subset of the given planks and assemble a $$$k$$$-step ladder using them?
The first line contains a single integer $$$T$$$ ($$$1 \le T \le 100$$$) — the number of queries. The queries are independent.
Each query consists of two lines. The first line contains a single integer $$$n$$$ ($$$2 \le n \le 10^5$$$) — the number of planks you have.
The second line contains $$$n$$$ integers $$$a_1, a_2, \dots, a_n$$$ ($$$1 \le a_i \le 10^5$$$) — the lengths of the corresponding planks.
It's guaranteed that the total number of planks from all queries doesn't exceed $$$10^5$$$.
Print $$$T$$$ integers — one per query. The $$$i$$$-th integer is the maximum number $$$k$$$, such that you can choose some subset of the planks given in the $$$i$$$-th query and assemble a $$$k$$$-step ladder using them.
Print $$$0$$$ if you can't make even $$$1$$$-step ladder from the given set of planks.
4 4 1 3 1 3 3 3 3 2 5 2 3 3 4 2 3 1 1 2
2 1 2 0
Examples for the queries $$$1-3$$$ are shown at the image in the legend section.
The Russian meme to express the quality of the ladders:

| Name |
|---|




