Polycarpus has a complex electronic device. The core of this device is a circuit board. The board has $$$10^9$$$ contact points which are numbered from $$$1$$$ to $$$10^9$$$. Also there are $$$n$$$ wires numbered from $$$1$$$ to $$$n$$$, each connecting two distinct contact points on the board. An electric signal can pass between wires $$$A$$$ and $$$B$$$ if:
- either both wires share the same contact point;
- or there is a sequence of wires starting with $$$A$$$ and ending with $$$B$$$, and each pair of adjacent wires in the sequence share a contact point.
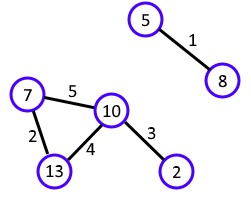 The picture shows a circuit board with $$$5$$$ wires. Contact points with numbers $$$2, 5, 7, 8, 10, 13$$$ are used. Here an electrical signal can pass from wire $$$2$$$ to wire $$$3$$$, but not to wire $$$1$$$.
The picture shows a circuit board with $$$5$$$ wires. Contact points with numbers $$$2, 5, 7, 8, 10, 13$$$ are used. Here an electrical signal can pass from wire $$$2$$$ to wire $$$3$$$, but not to wire $$$1$$$. Currently the circuit board is broken. Polycarpus thinks that the board could be fixed if the wires were re-soldered so that a signal could pass between any pair of wires.
It takes $$$1$$$ minute for Polycarpus to re-solder an end of a wire. I.e. it takes one minute to change one of the two contact points for a wire. Any contact point from range $$$[1, 10^9]$$$ can be used as a new contact point. A wire's ends must always be soldered to distinct contact points. Both wire's ends can be re-solded, but that will require two actions and will take $$$2$$$ minutes in total.
Find the minimum amount of time Polycarpus needs to re-solder wires so that a signal can pass between any pair of wires. Also output an optimal sequence of wire re-soldering.
The input contains one or several test cases. The first input line contains a single integer $$$t$$$ — number of test cases. Then, $$$t$$$ test cases follow.
The first line of each test case contains a single integer $$$n$$$ ($$$1 \le n \le 10^5$$$) — the number of wires. The following $$$n$$$ lines describe wires, each line containing two space-separated integers $$$x_i, y_i$$$ ($$$1 \le x_i, y_i \le 10^9$$$, $$$x_i \neq y_i$$$) — contact points connected by the $$$i$$$-th wire. A couple of contact points can be connected with more than one wire.
Sum of values of $$$n$$$ across all test cases does not exceed $$$10^5$$$.
For each test case first print one line with a single integer $$$k$$$ — the minimum number of minutes needed to re-solder wires so that a signal can pass between any pair of wires. In the following $$$k$$$ lines print the description of re-solderings. Each re-soldering should be described by three integers $$$w_j, a_j, b_j$$$ ($$$1 \le w_j \le n$$$, $$$1 \le a_j, b_j \le 10^9$$$). Such triple means that during the $$$j$$$-th re-soldering an end of the $$$w_j$$$-th wire, which was soldered to contact point $$$a_j$$$, becomes soldered to contact point $$$b_j$$$ instead. After each re-soldering of a wire it must connect two distinct contact points. If there are multiple optimal re-solderings, print any of them.
2 1 4 7 4 1 2 2 3 4 5 5 6
0 1 2 3 5
| Name |
|---|




