| Codeforces Round 600 (Div. 2) |
|---|
| Finished |
You're given a simple, undirected, connected, weighted graph with $$$n$$$ nodes and $$$m$$$ edges.
Nodes are numbered from $$$1$$$ to $$$n$$$. There are exactly $$$k$$$ centrals (recharge points), which are nodes $$$1, 2, \ldots, k$$$.
We consider a robot moving into this graph, with a battery of capacity $$$c$$$, not fixed by the constructor yet. At any time, the battery contains an integer amount $$$x$$$ of energy between $$$0$$$ and $$$c$$$ inclusive.
Traversing an edge of weight $$$w_i$$$ is possible only if $$$x \ge w_i$$$, and costs $$$w_i$$$ energy points ($$$x := x - w_i$$$).
Moreover, when the robot reaches a central, its battery is entirely recharged ($$$x := c$$$).
You're given $$$q$$$ independent missions, the $$$i$$$-th mission requires to move the robot from central $$$a_i$$$ to central $$$b_i$$$.
For each mission, you should tell the minimum capacity required to acheive it.
The first line contains four integers $$$n$$$, $$$m$$$, $$$k$$$ and $$$q$$$ ($$$2 \le k \le n \le 10^5$$$ and $$$1 \le m, q \le 3 \cdot 10^5$$$).
The $$$i$$$-th of the next $$$m$$$ lines contains three integers $$$u_i$$$, $$$v_i$$$ and $$$w_i$$$ ($$$1 \le u_i, v_i \le n$$$, $$$u_i \neq v_i$$$, $$$1 \le w_i \le 10^9$$$), that mean that there's an edge between nodes $$$u$$$ and $$$v$$$, with a weight $$$w_i$$$.
It is guaranteed that the given graph is simple (there is no self-loop, and there is at most one edge between every pair of nodes) and connected.
The $$$i$$$-th of the next $$$q$$$ lines contains two integers $$$a_i$$$ and $$$b_i$$$ ($$$1 \le a_i, b_i \le k$$$, $$$a_i \neq b_i$$$).
You have to output $$$q$$$ lines, where the $$$i$$$-th line contains a single integer : the minimum capacity required to acheive the $$$i$$$-th mission.
10 9 3 1 10 9 11 9 2 37 2 4 4 4 1 8 1 5 2 5 7 3 7 3 2 3 8 4 8 6 13 2 3
12
9 11 3 2 1 3 99 1 4 5 4 5 3 5 6 3 6 4 11 6 7 21 7 2 6 7 8 4 8 9 3 9 2 57 9 3 2 3 1 2 3
38 15
In the first example, the graph is the chain $$$10 - 9 - 2^C - 4 - 1^C - 5 - 7 - 3^C - 8 - 6$$$, where centrals are nodes $$$1$$$, $$$2$$$ and $$$3$$$.
For the mission $$$(2, 3)$$$, there is only one simple path possible. Here is a simulation of this mission when the capacity is $$$12$$$.
- The robot begins on the node $$$2$$$, with $$$c = 12$$$ energy points.
- The robot uses an edge of weight $$$4$$$.
- The robot reaches the node $$$4$$$, with $$$12 - 4 = 8$$$ energy points.
- The robot uses an edge of weight $$$8$$$.
- The robot reaches the node $$$1$$$ with $$$8 - 8 = 0$$$ energy points.
- The robot is on a central, so its battery is recharged. He has now $$$c = 12$$$ energy points.
- The robot uses an edge of weight $$$2$$$.
- The robot is on the node $$$5$$$, with $$$12 - 2 = 10$$$ energy points.
- The robot uses an edge of weight $$$3$$$.
- The robot is on the node $$$7$$$, with $$$10 - 3 = 7$$$ energy points.
- The robot uses an edge of weight $$$2$$$.
- The robot is on the node $$$3$$$, with $$$7 - 2 = 5$$$ energy points.
- The robot is on a central, so its battery is recharged. He has now $$$c = 12$$$ energy points.
- End of the simulation.
Note that if value of $$$c$$$ was lower than $$$12$$$, we would have less than $$$8$$$ energy points on node $$$4$$$, and we would be unable to use the edge $$$4 \leftrightarrow 1$$$ of weight $$$8$$$. Hence $$$12$$$ is the minimum capacity required to acheive the mission.
—
The graph of the second example is described here (centrals are red nodes):
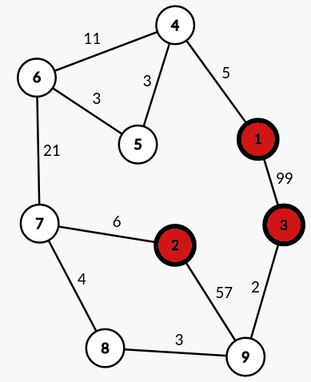
The robot can acheive the mission $$$(3, 1)$$$ with a battery of capacity $$$c = 38$$$, using the path $$$3 \rightarrow 9 \rightarrow 8 \rightarrow 7 \rightarrow 2 \rightarrow 7 \rightarrow 6 \rightarrow 5 \rightarrow 4 \rightarrow 1$$$
The robot can acheive the mission $$$(2, 3)$$$ with a battery of capacity $$$c = 15$$$, using the path $$$2 \rightarrow 7 \rightarrow 8 \rightarrow 9 \rightarrow 3$$$
| Name |
|---|




