| Codeforces Round 616 (Div. 1) |
|---|
| Finished |
Let's call two strings $$$s$$$ and $$$t$$$ anagrams of each other if it is possible to rearrange symbols in the string $$$s$$$ to get a string, equal to $$$t$$$.
Let's consider two strings $$$s$$$ and $$$t$$$ which are anagrams of each other. We say that $$$t$$$ is a reducible anagram of $$$s$$$ if there exists an integer $$$k \ge 2$$$ and $$$2k$$$ non-empty strings $$$s_1, t_1, s_2, t_2, \dots, s_k, t_k$$$ that satisfy the following conditions:
- If we write the strings $$$s_1, s_2, \dots, s_k$$$ in order, the resulting string will be equal to $$$s$$$;
- If we write the strings $$$t_1, t_2, \dots, t_k$$$ in order, the resulting string will be equal to $$$t$$$;
- For all integers $$$i$$$ between $$$1$$$ and $$$k$$$ inclusive, $$$s_i$$$ and $$$t_i$$$ are anagrams of each other.
If such strings don't exist, then $$$t$$$ is said to be an irreducible anagram of $$$s$$$. Note that these notions are only defined when $$$s$$$ and $$$t$$$ are anagrams of each other.
For example, consider the string $$$s = $$$ "gamegame". Then the string $$$t = $$$ "megamage" is a reducible anagram of $$$s$$$, we may choose for example $$$s_1 = $$$ "game", $$$s_2 = $$$ "gam", $$$s_3 = $$$ "e" and $$$t_1 = $$$ "mega", $$$t_2 = $$$ "mag", $$$t_3 = $$$ "e":
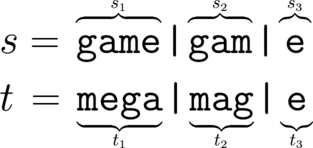
On the other hand, we can prove that $$$t = $$$ "memegaga" is an irreducible anagram of $$$s$$$.
You will be given a string $$$s$$$ and $$$q$$$ queries, represented by two integers $$$1 \le l \le r \le |s|$$$ (where $$$|s|$$$ is equal to the length of the string $$$s$$$). For each query, you should find if the substring of $$$s$$$ formed by characters from the $$$l$$$-th to the $$$r$$$-th has at least one irreducible anagram.
The first line contains a string $$$s$$$, consisting of lowercase English characters ($$$1 \le |s| \le 2 \cdot 10^5$$$).
The second line contains a single integer $$$q$$$ ($$$1 \le q \le 10^5$$$) — the number of queries.
Each of the following $$$q$$$ lines contain two integers $$$l$$$ and $$$r$$$ ($$$1 \le l \le r \le |s|$$$), representing a query for the substring of $$$s$$$ formed by characters from the $$$l$$$-th to the $$$r$$$-th.
For each query, print a single line containing "Yes" (without quotes) if the corresponding substring has at least one irreducible anagram, and a single line containing "No" (without quotes) otherwise.
aaaaa 3 1 1 2 4 5 5
Yes No Yes
aabbbbbbc 6 1 2 2 4 2 2 1 9 5 7 3 5
No Yes Yes Yes No No
In the first sample, in the first and third queries, the substring is "a", which has itself as an irreducible anagram since two or more non-empty strings cannot be put together to obtain "a". On the other hand, in the second query, the substring is "aaa", which has no irreducible anagrams: its only anagram is itself, and we may choose $$$s_1 = $$$ "a", $$$s_2 = $$$ "aa", $$$t_1 = $$$ "a", $$$t_2 = $$$ "aa" to show that it is a reducible anagram.
In the second query of the second sample, the substring is "abb", which has, for example, "bba" as an irreducible anagram.
| Name |
|---|




