| Codeforces Round 615 (Div. 3) |
|---|
| Finished |
You are given an unweighted tree with $$$n$$$ vertices. Recall that a tree is a connected undirected graph without cycles.
Your task is to choose three distinct vertices $$$a, b, c$$$ on this tree such that the number of edges which belong to at least one of the simple paths between $$$a$$$ and $$$b$$$, $$$b$$$ and $$$c$$$, or $$$a$$$ and $$$c$$$ is the maximum possible. See the notes section for a better understanding.
The simple path is the path that visits each vertex at most once.
The first line contains one integer number $$$n$$$ ($$$3 \le n \le 2 \cdot 10^5$$$) — the number of vertices in the tree.
Next $$$n - 1$$$ lines describe the edges of the tree in form $$$a_i, b_i$$$ ($$$1 \le a_i$$$, $$$b_i \le n$$$, $$$a_i \ne b_i$$$). It is guaranteed that given graph is a tree.
In the first line print one integer $$$res$$$ — the maximum number of edges which belong to at least one of the simple paths between $$$a$$$ and $$$b$$$, $$$b$$$ and $$$c$$$, or $$$a$$$ and $$$c$$$.
In the second line print three integers $$$a, b, c$$$ such that $$$1 \le a, b, c \le n$$$ and $$$a \ne, b \ne c, a \ne c$$$.
If there are several answers, you can print any.
8 1 2 2 3 3 4 4 5 4 6 3 7 3 8
5 1 8 6
The picture corresponding to the first example (and another one correct answer):
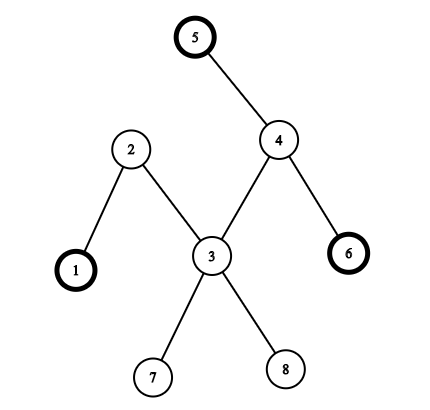
If you choose vertices $$$1, 5, 6$$$ then the path between $$$1$$$ and $$$5$$$ consists of edges $$$(1, 2), (2, 3), (3, 4), (4, 5)$$$, the path between $$$1$$$ and $$$6$$$ consists of edges $$$(1, 2), (2, 3), (3, 4), (4, 6)$$$ and the path between $$$5$$$ and $$$6$$$ consists of edges $$$(4, 5), (4, 6)$$$. The union of these paths is $$$(1, 2), (2, 3), (3, 4), (4, 5), (4, 6)$$$ so the answer is $$$5$$$. It can be shown that there is no better answer.
| Name |
|---|




