| Codeforces Round 103 (Div. 2) |
|---|
| Finished |
The secondary diagonal of a square matrix is a diagonal going from the top right to the bottom left corner. Let's define an n-degree staircase as a square matrix n × n containing no squares above the secondary diagonal (the picture below shows a 5-degree staircase).

The squares of the n-degree staircase contain m sportsmen.
A sportsman needs one second to move to a side-neighboring square of the staircase. Before the beginning of the competition each sportsman must choose one of the shortest ways to the secondary diagonal.
After the starting whistle the competition begins and all sportsmen start moving along the chosen paths. When a sportsman reaches a cell of the secondary diagonal, he stops and moves no more. The competition ends when all sportsmen reach the secondary diagonal. The competition is considered successful if during it no two sportsmen were present in the same square simultaneously. Any square belonging to the secondary diagonal also cannot contain more than one sportsman. If a sportsman at the given moment of time leaves a square and another sportsman comes to it, then they are not considered to occupy the same square simultaneously. Note that other extreme cases (for example, two sportsmen moving towards each other) are impossible as the chosen ways are the shortest ones.
You are given positions of m sportsmen on the staircase. Your task is to choose among them the maximum number of sportsmen for who the competition can be successful, that is, so that there existed such choice of shortest ways for the sportsmen at which no two sportsmen find themselves in the same square simultaneously. All other sportsmen that are not chosen will be removed from the staircase before the competition starts.
The first line contains two integers n and m (1 ≤ n, m ≤ 105). Then m lines contain coordinates of sportsmen on the staircase as pairs of integers ri, ci (1 ≤ ri, ci ≤ n, n - ci < ri), where ri is the number of the staircase row, ci is the number of the staircase column (to understand the principle of numbering rows and columns see the explanatory pictures). No two sportsmen stand on the same square of the staircase.
In the first line print the number of the chosen sportsmen. In the second line print the numbers of chosen sportsmen in any order, separating the numbers with spaces. If there are several answers, you are permitted to print any of them. The sportsmen are numbered starting from one in the order in which they are given in the input data.
3 3
2 3
3 2
3 3
3
1 2 3
A note to the first sample.
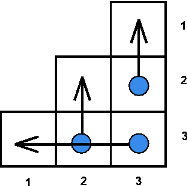
| Name |
|---|




