→ Attention
The package for this problem was not updated by the problem writer or Codeforces administration after we've upgraded the judging servers. To adjust the time limit constraint, a solution execution time will be multiplied by 2. For example, if your solution works for 400 ms on judging servers, then the value 800 ms will be displayed and used to determine the verdict.
| Codeforces Round 139 (Div. 2) |
|---|
| Finished |
→ Virtual participation
Virtual contest is a way to take part in past contest, as close as possible to participation on time. It is supported only ICPC mode for virtual contests.
If you've seen these problems, a virtual contest is not for you - solve these problems in the archive.
If you just want to solve some problem from a contest, a virtual contest is not for you - solve this problem in the archive.
Never use someone else's code, read the tutorials or communicate with other person during a virtual contest.
→ Problem tags
math
number theory
*2100
No tag edit access
→ Contest materials
The problem statement has recently been changed. View the changes.
×
E. Unsolvable
time limit per test
2 secondsmemory limit per test
256 megabytesinput
standard inputoutput
standard outputConsider the following equation:
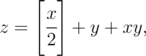
Let's find all integer z (z > 0), for which this equation is unsolvable in positive integers. The phrase "unsolvable in positive integers" means that there are no such positive integers x and y (x, y > 0), for which the given above equation holds.
Let's write out all such z in the increasing order: z1, z2, z3, and so on (zi < zi + 1). Your task is: given the number n, find the number zn.
Input
The first line contains a single integer n (1 ≤ n ≤ 40).
Output
Print a single integer — the number zn modulo 1000000007 (109 + 7). It is guaranteed that the answer exists.
Examples
Input
1
Output
1
Input
2
Output
3
Input
3
Output
15
Codeforces (c) Copyright 2010-2024 Mike Mirzayanov
The only programming contests Web 2.0 platform
Server time: Apr/27/2024 14:31:01 (i1).
Desktop version, switch to mobile version.
Supported by
User lists


| Name |
|---|




