| Codeforces Round 155 (Div. 2) |
|---|
| Finished |
Rats have bred to hundreds and hundreds in the basement of the store, owned by Vasily Petrovich. Vasily Petrovich may have not noticed their presence, but they got into the habit of sneaking into the warehouse and stealing food from there. Vasily Petrovich cannot put up with it anymore, he has to destroy the rats in the basement. Since mousetraps are outdated and do not help, and rat poison can poison inattentive people as well as rats, he chose a radical way: to blow up two grenades in the basement (he does not have more).
In this problem, we will present the shop basement as a rectangular table of n × m cells. Some of the cells are occupied by walls, and the rest of them are empty. Vasily has been watching the rats and he found out that at a certain time they go to sleep, and all the time they sleep in the same places. He wants to blow up a grenade when this convenient time comes. On the plan of his basement, he marked cells with sleeping rats in them. Naturally, these cells are not occupied by walls.
Grenades can only blow up in a cell that is not occupied by a wall. The blast wave from a grenade distributes as follows. We assume that the grenade blast occurs at time 0. During this initial time only the cell where the grenade blew up gets 'clear'. If at time t some cell is clear, then at time t + 1 those side-neighbouring cells which are not occupied by the walls get clear too (some of them could have been cleared before). The blast wave distributes for exactly d seconds, then it dies immediately.
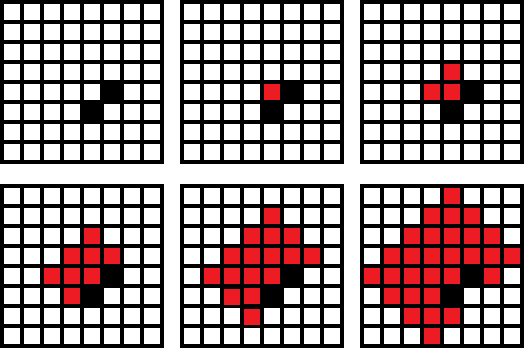 An example of a distributing blast wave: Picture 1 shows the situation before the blast, and the following pictures show "clear" cells by time 0,1,2,3 and 4. Thus, the blast wave on the picture distributes for d = 4 seconds.
An example of a distributing blast wave: Picture 1 shows the situation before the blast, and the following pictures show "clear" cells by time 0,1,2,3 and 4. Thus, the blast wave on the picture distributes for d = 4 seconds. Vasily Petrovich wonders, whether he can choose two cells to blast the grenades so as to clear all cells with sleeping rats. Write the program that finds it out.
The first line contains three integers n, m and d, separated by single spaces (4 ≤ n, m ≤ 1000, 1 ≤ d ≤ 8). Next n lines contain the table that represents the basement plan. Each row of the table consists of m characters. Character "X" means that the corresponding cell is occupied by the wall, character "." represents a empty cell, character "R" represents a empty cell with sleeping rats.
It is guaranteed that the first and the last row, as well as the first and the last column consist of characters "X". The plan has at least two empty cells. There is at least one cell with sleeping rats.
If it is impossible to blow up all cells with sleeping rats, print a single integer -1. Otherwise, print four space-separated integers r1, c1, r2, c2, that mean that one grenade should go off in cell (r1, c1), and the other one — in cell (r2, c2).
Consider the table rows numbered from top to bottom from 1 to n and the table columns — from left to right from 1 to m. As r1 and r2 represent the row numbers, and c1 and c2 represent the column numbers in the table, they should fit the limits: 1 ≤ r1, r2 ≤ n, 1 ≤ c1, c2 ≤ m. It is forbidden to blow a grenade twice in the same cell. The blast waves of the grenades can intersect. It is possible that one grenade blast destroys no rats, and the other one destroys all of them.
4 4 1
XXXX
XR.X
X.RX
XXXX
2 2 2 3
9 14 5
XXXXXXXXXXXXXX
X....R...R...X
X..R.........X
X....RXR..R..X
X..R...X.....X
XR.R...X.....X
X....XXR.....X
X....R..R.R..X
XXXXXXXXXXXXXX
2 3 6 9
7 7 1
XXXXXXX
X.R.R.X
X.....X
X..X..X
X..R..X
X....RX
XXXXXXX
-1
| Name |
|---|




