| Codeforces Round 175 (Div. 2) |
|---|
| Finished |
Permutation p is an ordered set of integers p1, p2, ..., pn, consisting of n distinct positive integers, each of them doesn't exceed n. We'll denote the i-th element of permutation p as pi. We'll call number n the size or the length of permutation p1, p2, ..., pn.
Petya decided to introduce the sum operation on the set of permutations of length n. Let's assume that we are given two permutations of length n: a1, a2, ..., an and b1, b2, ..., bn. Petya calls the sum of permutations a and b such permutation c of length n, where ci = ((ai - 1 + bi - 1) mod n) + 1 (1 ≤ i ≤ n).
Operation 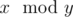 means taking the remainder after dividing number x by number y.
means taking the remainder after dividing number x by number y.
Obviously, not for all permutations a and b exists permutation c that is sum of a and b. That's why Petya got sad and asked you to do the following: given n, count the number of such pairs of permutations a and b of length n, that exists permutation c that is sum of a and b. The pair of permutations x, y (x ≠ y) and the pair of permutations y, x are considered distinct pairs.
As the answer can be rather large, print the remainder after dividing it by 1000000007 (109 + 7).
The single line contains integer n (1 ≤ n ≤ 16).
In the single line print a single non-negative integer — the number of such pairs of permutations a and b, that exists permutation c that is sum of a and b, modulo 1000000007 (109 + 7).
3
18
5
1800
| Name |
|---|




