| Codeforces Round 185 (Div. 1) |
|---|
| Finished |
Rainbow built h cells in a row that are numbered from 1 to h from left to right. There are n cells with treasure. We call each of these n cells "Treasure Cell". The i-th "Treasure Cell" is the ai-th cell and the value of treasure in it is ci dollars.
Then, Freda went in the first cell. For now, she can go just k cells forward, or return to the first cell. That means Freda was able to reach the 1st, (k + 1)-th, (2·k + 1)-th, (3·k + 1)-th cells and so on.
Then Rainbow gave Freda m operations. Each operation is one of the following three types:
- Add another method x: she can also go just x cells forward at any moment. For example, initially she has only one method k. If at some moment she has methods a1, a2, ..., ar then she can reach all the cells with number in form
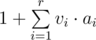 , where vi — some non-negative integer.
, where vi — some non-negative integer. - Reduce the value of the treasure in the x-th "Treasure Cell" by y dollars. In other words, to apply assignment cx = cx - y.
- Ask the value of the most valuable treasure among the cells Freda can reach. If Freda cannot reach any cell with the treasure then consider the value of the most valuable treasure equal to 0, and do nothing. Otherwise take the most valuable treasure away. If several "Treasure Cells" have the most valuable treasure, take the "Treasure Cell" with the minimum number (not necessarily with the minimum number of cell). After that the total number of cells with a treasure is decreased by one.
As a programmer, you are asked by Freda to write a program to answer each query.
The first line of the input contains four integers: h (1 ≤ h ≤ 1018), n, m (1 ≤ n, m ≤ 105) and k (1 ≤ k ≤ 104).
Each of the next n lines contains two integers: ai (1 ≤ ai ≤ h), ci (1 ≤ ci ≤ 109). That means the i-th "Treasure Cell" is the ai-th cell and cost of the treasure in that cell is ci dollars. All the ai are distinct.
Each of the next m lines is in one of the three following formats:
- "1 x" — an operation of type 1, 1 ≤ x ≤ h;
- "2 x y" — an operation of type 2, 1 ≤ x ≤ n, 0 ≤ y < cx;
- "3" — an operation of type 3.
There are at most 20 operations of type 1. It's guaranteed that at any moment treasure in each cell has positive value. It's guaranteed that all operations is correct (no operation can decrease the value of the taken tresure).
Please, do not use the %lld specifier to read 64-bit integers in С++. It is preferred to use the cin, cout streams or the %I64d specifier.
For each operation of type 3, output an integer indicates the value (in dollars) of the most valuable treasure among the "Treasure Cells" Freda can reach. If there is no such treasure, output 0.
10 3 5 2
5 50
7 60
8 100
2 2 5
3
1 3
3
3
55
100
50
In the sample, there are 10 cells and 3 "Treasure Cells". The first "Treasure Cell" is cell 5, having 50 dollars tresure in it. The second "Treasure Cell" is cell 7, having 60 dollars tresure in it. The third "Treasure Cell" is cell 8, having 100 dollars tresure in it.
At first, Freda can only reach cell 1, 3, 5, 7 and 9. In the first operation, we reduce the value in the second "Treasure Cell" from 60 to 55. Then the most valuable treasure among the "Treasure Cells" she can reach is max(50, 55) = 55. After the third operation, she can also go 3 cells forward each step, being able to reach cell 1, 3, 4, 5, 6, 7, 8, 9, 10. So the most valuable tresure is 100.
Noticed that she took the 55 dollars and 100 dollars treasure away, so the last answer is 50.
| Name |
|---|




