| Codeforces Round 190 (Div. 1) |
|---|
| Finished |
Fox Ciel is in the Amusement Park. And now she is in a queue in front of the Ferris wheel. There are n people (or foxes more precisely) in the queue: we use first people to refer one at the head of the queue, and n-th people to refer the last one in the queue.
There will be k gondolas, and the way we allocate gondolas looks like this:
- When the first gondolas come, the q1 people in head of the queue go into the gondolas.
- Then when the second gondolas come, the q2 people in head of the remain queue go into the gondolas.
...
- The remain qk people go into the last (k-th) gondolas.
Note that q1, q2, ..., qk must be positive. You can get from the statement that 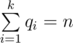 and qi > 0.
and qi > 0.
You know, people don't want to stay with strangers in the gondolas, so your task is to find an optimal allocation way (that is find an optimal sequence q) to make people happy. For every pair of people i and j, there exists a value uij denotes a level of unfamiliar. You can assume uij = uji for all i, j (1 ≤ i, j ≤ n) and uii = 0 for all i (1 ≤ i ≤ n). Then an unfamiliar value of a gondolas is the sum of the levels of unfamiliar between any pair of people that is into the gondolas.
A total unfamiliar value is the sum of unfamiliar values for all gondolas. Help Fox Ciel to find the minimal possible total unfamiliar value for some optimal allocation.
The first line contains two integers n and k (1 ≤ n ≤ 4000 and 1 ≤ k ≤ min(n, 800)) — the number of people in the queue and the number of gondolas. Each of the following n lines contains n integers — matrix u, (0 ≤ uij ≤ 9, uij = uji and uii = 0).
Please, use fast input methods (for example, please use BufferedReader instead of Scanner for Java).
Print an integer — the minimal possible total unfamiliar value.
5 2
0 0 1 1 1
0 0 1 1 1
1 1 0 0 0
1 1 0 0 0
1 1 0 0 0
0
8 3
0 1 1 1 1 1 1 1
1 0 1 1 1 1 1 1
1 1 0 1 1 1 1 1
1 1 1 0 1 1 1 1
1 1 1 1 0 1 1 1
1 1 1 1 1 0 1 1
1 1 1 1 1 1 0 1
1 1 1 1 1 1 1 0
7
3 2
0 2 0
2 0 3
0 3 0
2
In the first example, we can allocate people like this: {1, 2} goes into a gondolas, {3, 4, 5} goes into another gondolas.
In the second example, an optimal solution is : {1, 2, 3} | {4, 5, 6} | {7, 8}.
| Name |
|---|




