| Codeforces Round 226 (Div. 2) |
|---|
| Finished |
Recently, the bear started studying data structures and faced the following problem.
You are given a sequence of integers x1, x2, ..., xn of length n and m queries, each of them is characterized by two integers li, ri. Let's introduce f(p) to represent the number of such indexes k, that xk is divisible by p. The answer to the query li, ri is the sum: 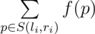 , where S(li, ri) is a set of prime numbers from segment [li, ri] (both borders are included in the segment).
, where S(li, ri) is a set of prime numbers from segment [li, ri] (both borders are included in the segment).
Help the bear cope with the problem.
The first line contains integer n (1 ≤ n ≤ 106). The second line contains n integers x1, x2, ..., xn (2 ≤ xi ≤ 107). The numbers are not necessarily distinct.
The third line contains integer m (1 ≤ m ≤ 50000). Each of the following m lines contains a pair of space-separated integers, li and ri (2 ≤ li ≤ ri ≤ 2·109) — the numbers that characterize the current query.
Print m integers — the answers to the queries on the order the queries appear in the input.
6
5 5 7 10 14 15
3
2 11
3 12
4 4
9
7
0
7
2 3 5 7 11 4 8
2
8 10
2 123
0
7
Consider the first sample. Overall, the first sample has 3 queries.
- The first query l = 2, r = 11 comes. You need to count f(2) + f(3) + f(5) + f(7) + f(11) = 2 + 1 + 4 + 2 + 0 = 9.
- The second query comes l = 3, r = 12. You need to count f(3) + f(5) + f(7) + f(11) = 1 + 4 + 2 + 0 = 7.
- The third query comes l = 4, r = 4. As this interval has no prime numbers, then the sum equals 0.
| Name |
|---|




