| Codeforces Round 232 (Div. 1) |
|---|
| Finished |
You are given a permutation p. Calculate the total number of inversions in all permutations that lexicographically do not exceed the given one.
As this number can be very large, print it modulo 1000000007 (109 + 7).
The first line contains a single integer n (1 ≤ n ≤ 106) — the length of the permutation. The second line contains n distinct integers p1, p2, ..., pn (1 ≤ pi ≤ n).
Print a single number — the answer to the problem modulo 1000000007 (109 + 7).
2
2 1
1
3
2 1 3
2
Permutation p of length n is the sequence that consists of n distinct integers, each of them is from 1 to n.
An inversion of permutation p1, p2, ..., pn is a pair of indexes (i, j), such that i < j and pi > pj.
Permutation a do not exceed permutation b lexicographically, if either a = b or there exists such number i, for which the following logical condition fulfills: 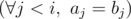 AND (ai < bi).
AND (ai < bi).
| Name |
|---|




