| Codeforces Round 250 (Div. 1) |
|---|
| Finished |
Our child likes computer science very much, especially he likes binary trees.
Consider the sequence of n distinct positive integers: c1, c2, ..., cn. The child calls a vertex-weighted rooted binary tree good if and only if for every vertex v, the weight of v is in the set {c1, c2, ..., cn}. Also our child thinks that the weight of a vertex-weighted tree is the sum of all vertices' weights.
Given an integer m, can you for all s (1 ≤ s ≤ m) calculate the number of good vertex-weighted rooted binary trees with weight s? Please, check the samples for better understanding what trees are considered different.
We only want to know the answer modulo 998244353 (7 × 17 × 223 + 1, a prime number).
The first line contains two integers n, m (1 ≤ n ≤ 105; 1 ≤ m ≤ 105). The second line contains n space-separated pairwise distinct integers c1, c2, ..., cn. (1 ≤ ci ≤ 105).
Print m lines, each line containing a single integer. The i-th line must contain the number of good vertex-weighted rooted binary trees whose weight exactly equal to i. Print the answers modulo 998244353 (7 × 17 × 223 + 1, a prime number).
2 3
1 2
1
3
9
3 10
9 4 3
0
0
1
1
0
2
4
2
6
15
5 10
13 10 6 4 15
0
0
0
1
0
1
0
2
0
5
In the first example, there are 9 good vertex-weighted rooted binary trees whose weight exactly equal to 3:
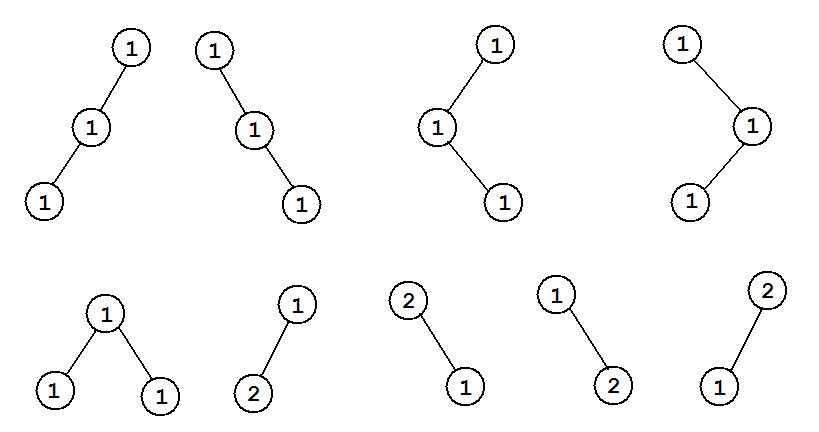
| Name |
|---|




