| Codeforces Round 275 (Div. 1) |
|---|
| Finished |
You play the game with your friend. The description of this game is listed below.
Your friend creates n distinct strings of the same length m and tells you all the strings. Then he randomly chooses one of them. He chooses strings equiprobably, i.e. the probability of choosing each of the n strings equals  . You want to guess which string was chosen by your friend.
. You want to guess which string was chosen by your friend.
In order to guess what string your friend has chosen, you are allowed to ask him questions. Each question has the following form: «What character stands on position pos in the string you have chosen?» A string is considered guessed when the answers to the given questions uniquely identify the string. After the string is guessed, you stop asking questions.
You do not have a particular strategy, so as each question you equiprobably ask about a position that hasn't been yet mentioned. Your task is to determine the expected number of questions needed to guess the string chosen by your friend.
The first line contains a single integer n (1 ≤ n ≤ 50) — the number of strings your friend came up with.
The next n lines contain the strings that your friend has created. It is guaranteed that all the strings are distinct and only consist of large and small English letters. Besides, the lengths of all strings are the same and are between 1 to 20 inclusive.
Print the single number — the expected value. Your answer will be considered correct if its absolute or relative error doesn't exceed 10 - 9.
2
aab
aac
2.000000000000000
3
aaA
aBa
Caa
1.666666666666667
3
aca
vac
wqq
1.000000000000000
In the first sample the strings only differ in the character in the third position. So only the following situations are possible:
- you guess the string in one question. The event's probability is
 ;
; - you guess the string in two questions. The event's probability is
 ·
·  =
=  (as in this case the first question should ask about the position that is other than the third one);
(as in this case the first question should ask about the position that is other than the third one); - you guess the string in three questions. The event's probability is
 ·
·  ·
·  =
=  ;
;
Thus, the expected value is equal to 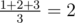
In the second sample we need at most two questions as any pair of questions uniquely identifies the string. So the expected number of questions is 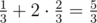 .
.
In the third sample whatever position we ask about in the first question, we immediately identify the string.
| Name |
|---|




