| Codeforces Round 277 (Div. 2) |
|---|
| Finished |
Let's define logical OR as an operation on two logical values (i. e. values that belong to the set {0, 1}) that is equal to 1 if either or both of the logical values is set to 1, otherwise it is 0. We can define logical OR of three or more logical values in the same manner:
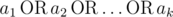 where
where 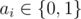 is equal to 1 if some ai = 1, otherwise it is equal to 0.
is equal to 1 if some ai = 1, otherwise it is equal to 0.
Nam has a matrix A consisting of m rows and n columns. The rows are numbered from 1 to m, columns are numbered from 1 to n. Element at row i (1 ≤ i ≤ m) and column j (1 ≤ j ≤ n) is denoted as Aij. All elements of A are either 0 or 1. From matrix A, Nam creates another matrix B of the same size using formula:
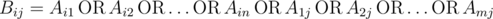 .
.
(Bij is OR of all elements in row i and column j of matrix A)
Nam gives you matrix B and challenges you to guess matrix A. Although Nam is smart, he could probably make a mistake while calculating matrix B, since size of A can be large.
The first line contains two integer m and n (1 ≤ m, n ≤ 100), number of rows and number of columns of matrices respectively.
The next m lines each contain n integers separated by spaces describing rows of matrix B (each element of B is either 0 or 1).
In the first line, print "NO" if Nam has made a mistake when calculating B, otherwise print "YES". If the first line is "YES", then also print m rows consisting of n integers representing matrix A that can produce given matrix B. If there are several solutions print any one.
2 2
1 0
0 0
NO
2 3
1 1 1
1 1 1
YES
1 1 1
1 1 1
2 3
0 1 0
1 1 1
YES
0 0 0
0 1 0
| Name |
|---|




