| Codeforces Round 282 (Div. 1) |
|---|
| Finished |
Ali is Hamed's little brother and tomorrow is his birthday. Hamed wants his brother to earn his gift so he gave him a hard programming problem and told him if he can successfully solve it, he'll get him a brand new laptop. Ali is not yet a very talented programmer like Hamed and although he usually doesn't cheat but this time is an exception. It's about a brand new laptop. So he decided to secretly seek help from you. Please solve this problem for Ali.
An n-vertex weighted rooted tree is given. Vertex number 1 is a root of the tree. We define d(u, v) as the sum of edges weights on the shortest path between vertices u and v. Specifically we define d(u, u) = 0. Also let's define S(v) for each vertex v as a set containing all vertices u such that d(1, u) = d(1, v) + d(v, u). Function f(u, v) is then defined using the following formula:
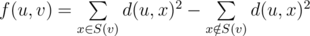
The goal is to calculate f(u, v) for each of the q given pair of vertices. As the answer can be rather large it's enough to print it modulo 109 + 7.
In the first line of input an integer n (1 ≤ n ≤ 105), number of vertices of the tree is given.
In each of the next n - 1 lines three space-separated integers ai, bi, ci (1 ≤ ai, bi ≤ n, 1 ≤ ci ≤ 109) are given indicating an edge between ai and bi with weight equal to ci.
In the next line an integer q (1 ≤ q ≤ 105), number of vertex pairs, is given.
In each of the next q lines two space-separated integers ui, vi (1 ≤ ui, vi ≤ n) are given meaning that you must calculate f(ui, vi).
It is guaranteed that the given edges form a tree.
Output q lines. In the i-th line print the value of f(ui, vi) modulo 109 + 7.
5
1 2 1
4 3 1
3 5 1
1 3 1
5
1 1
1 5
2 4
2 1
3 5
10
1000000005
1000000002
23
1000000002
8
1 2 100
1 3 20
2 4 2
2 5 1
3 6 1
3 7 2
6 8 5
6
1 8
2 3
5 8
2 6
4 7
6 1
999968753
49796
999961271
999991235
999958569
45130
| Name |
|---|




