| Codeforces Round 283 (Div. 1) |
|---|
| Finished |
Assume that sk(n) equals the sum of digits of number n in the k-based notation. For example, s2(5) = s2(1012) = 1 + 0 + 1 = 2, s3(14) = s3(1123) = 1 + 1 + 2 = 4.
The sequence of integers a0, ..., an - 1 is defined as 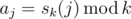 . Your task is to calculate the number of distinct subsequences of sequence a0, ..., an - 1. Calculate the answer modulo 109 + 7.
. Your task is to calculate the number of distinct subsequences of sequence a0, ..., an - 1. Calculate the answer modulo 109 + 7.
Sequence a1, ..., ak is called to be a subsequence of sequence b1, ..., bl, if there is a sequence of indices 1 ≤ i1 < ... < ik ≤ l, such that a1 = bi1, ..., ak = bik. In particular, an empty sequence (i.e. the sequence consisting of zero elements) is a subsequence of any sequence.
The first line contains two space-separated numbers n and k (1 ≤ n ≤ 1018, 2 ≤ k ≤ 30).
In a single line print the answer to the problem modulo 109 + 7.
4 2
11
7 7
128
In the first sample the sequence ai looks as follows: (0, 1, 1, 0). All the possible subsequences are:
In the second sample the sequence ai looks as follows: (0, 1, 2, 3, 4, 5, 6). The subsequences of this sequence are exactly all increasing sequences formed from numbers from 0 to 6. It is easy to see that there are 27 = 128 such sequences.
| Name |
|---|




