| Looksery Cup 2015 |
|---|
| Finished |
The determinant of a matrix 2 × 2 is defined as follows:
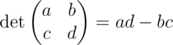
A matrix is called degenerate if its determinant is equal to zero.
The norm ||A|| of a matrix A is defined as a maximum of absolute values of its elements.
You are given a matrix 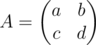 . Consider any degenerate matrix B such that norm ||A - B|| is minimum possible. Determine ||A - B||.
. Consider any degenerate matrix B such that norm ||A - B|| is minimum possible. Determine ||A - B||.
The first line contains two integers a and b (|a|, |b| ≤ 109), the elements of the first row of matrix A.
The second line contains two integers c and d (|c|, |d| ≤ 109) the elements of the second row of matrix A.
Output a single real number, the minimum possible value of ||A - B||. Your answer is considered to be correct if its absolute or relative error does not exceed 10 - 9.
1 2
3 4
0.2000000000
1 0
0 1
0.5000000000
In the first sample matrix B is 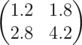
In the second sample matrix B is 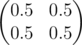
| Name |
|---|




