| Codeforces Round 324 (Div. 2) |
|---|
| Finished |
Kolya loves putting gnomes at the circle table and giving them coins, and Tanya loves studying triplets of gnomes, sitting in the vertexes of an equilateral triangle.
More formally, there are 3n gnomes sitting in a circle. Each gnome can have from 1 to 3 coins. Let's number the places in the order they occur in the circle by numbers from 0 to 3n - 1, let the gnome sitting on the i-th place have ai coins. If there is an integer i (0 ≤ i < n) such that ai + ai + n + ai + 2n ≠ 6, then Tanya is satisfied.
Count the number of ways to choose ai so that Tanya is satisfied. As there can be many ways of distributing coins, print the remainder of this number modulo 109 + 7. Two ways, a and b, are considered distinct if there is index i (0 ≤ i < 3n), such that ai ≠ bi (that is, some gnome got different number of coins in these two ways).
A single line contains number n (1 ≤ n ≤ 105) — the number of the gnomes divided by three.
Print a single number — the remainder of the number of variants of distributing coins that satisfy Tanya modulo 109 + 7.
1
20
2
680
20 ways for n = 1 (gnome with index 0 sits on the top of the triangle, gnome 1 on the right vertex, gnome 2 on the left vertex): 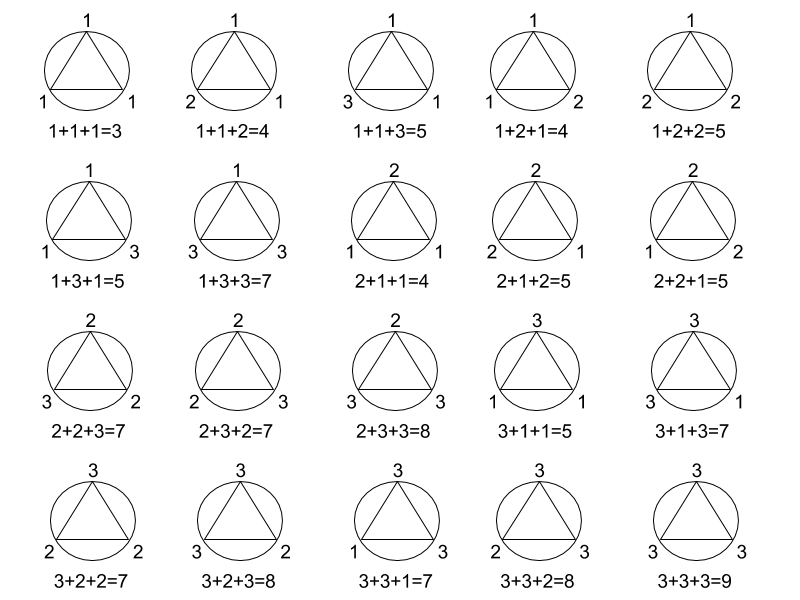
| Name |
|---|




