| Codeforces Round 336 (Div. 2) |
|---|
| Finished |
Genos needs your help. He was asked to solve the following programming problem by Saitama:
The length of some string s is denoted |s|. The Hamming distance between two strings s and t of equal length is defined as 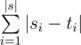 , where si is the i-th character of s and ti is the i-th character of t. For example, the Hamming distance between string "0011" and string "0110" is |0 - 0| + |0 - 1| + |1 - 1| + |1 - 0| = 0 + 1 + 0 + 1 = 2.
, where si is the i-th character of s and ti is the i-th character of t. For example, the Hamming distance between string "0011" and string "0110" is |0 - 0| + |0 - 1| + |1 - 1| + |1 - 0| = 0 + 1 + 0 + 1 = 2.
Given two binary strings a and b, find the sum of the Hamming distances between a and all contiguous substrings of b of length |a|.
The first line of the input contains binary string a (1 ≤ |a| ≤ 200 000).
The second line of the input contains binary string b (|a| ≤ |b| ≤ 200 000).
Both strings are guaranteed to consist of characters '0' and '1' only.
Print a single integer — the sum of Hamming distances between a and all contiguous substrings of b of length |a|.
01
00111
3
0011
0110
2
For the first sample case, there are four contiguous substrings of b of length |a|: "00", "01", "11", and "11". The distance between "01" and "00" is |0 - 0| + |1 - 0| = 1. The distance between "01" and "01" is |0 - 0| + |1 - 1| = 0. The distance between "01" and "11" is |0 - 1| + |1 - 1| = 1. Last distance counts twice, as there are two occurrences of string "11". The sum of these edit distances is 1 + 0 + 1 + 1 = 3.
The second sample case is described in the statement.
| Name |
|---|




