| AIM Tech Round (Div. 1) |
|---|
| Finished |
A MIPT student named Misha has a birthday today, and he decided to celebrate it in his country house in suburban Moscow. n friends came by, and after a typical party they decided to play blind man's buff.
The birthday boy gets blindfolded and the other players scatter around the house. The game is played in several rounds. In each round, Misha catches exactly one of his friends and has to guess who it is. The probability of catching the i-th friend does not change between rounds and is equal to pi percent (as we know, it is directly proportional to the amount of alcohol consumed by the i-th friend) and p1 + p2 + ... + pn = 100 holds. Misha has no information about who he caught. After Misha makes an attempt to guess the caught person, the round ends. Even then, Misha isn't told whether he guessed correctly, and a new round begins.
The game ends when Misha guesses every friend at least once, that is, there exists such set of rounds k1, k2, ..., kn, that during round number ki Misha caught the i-th friend and guessed him. Misha wants to minimize the expectation of the number of rounds of the game. Despite the fact that at any point in the game Misha has no information about who he has already guessed, his friends are honest, and if they see that the condition for the end of the game is fulfilled, the game ends immediately. Find the expectation of the number of rounds in the game if Misha plays optimally.
The first line of the input contains a single integer n (1 ≤ n ≤ 100) — the number of Misha's friends.
The second line contains n integers pi (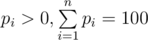 ), giving the probability to catch the i-th friend in one particular round in percent.
), giving the probability to catch the i-th friend in one particular round in percent.
Print a single real value — the expectation of the number of rounds provided that Misha plays optimally. Your answer will be considered correct if its absolute or relative error does not exceed 10 - 6.
Namely: let's assume that your answer is a, and the answer of the jury is b. The checker program will consider your answer correct, if 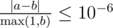 .
.
2
50 50
5.0000000000
4
50 20 20 10
39.2846263444
The optimal strategy in the first sample is to guess friends alternately.
| Name |
|---|




