| Codeforces Round 384 (Div. 2) |
|---|
| Finished |
Vladik was bored on his way home and decided to play the following game. He took n cards and put them in a row in front of himself. Every card has a positive integer number not exceeding 8 written on it. He decided to find the longest subsequence of cards which satisfies the following conditions:
- the number of occurrences of each number from 1 to 8 in the subsequence doesn't differ by more then 1 from the number of occurrences of any other number. Formally, if there are ck cards with number k on them in the subsequence, than for all pairs of integers
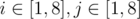 the condition |ci - cj| ≤ 1 must hold.
the condition |ci - cj| ≤ 1 must hold. - if there is at least one card with number x on it in the subsequence, then all cards with number x in this subsequence must form a continuous segment in it (but not necessarily a continuous segment in the original sequence). For example, the subsequence [1, 1, 2, 2] satisfies this condition while the subsequence [1, 2, 2, 1] doesn't. Note that [1, 1, 2, 2] doesn't satisfy the first condition.
Please help Vladik to find the length of the longest subsequence that satisfies both conditions.
The first line contains single integer n (1 ≤ n ≤ 1000) — the number of cards in Vladik's sequence.
The second line contains the sequence of n positive integers not exceeding 8 — the description of Vladik's sequence.
Print single integer — the length of the longest subsequence of Vladik's sequence that satisfies both conditions.
3
1 1 1
1
8
8 7 6 5 4 3 2 1
8
24
1 8 1 2 8 2 3 8 3 4 8 4 5 8 5 6 8 6 7 8 7 8 8 8
17
In the first sample all the numbers written on the cards are equal, so you can't take more than one card, otherwise you'll violate the first condition.
| Name |
|---|




