| VK Cup 2017 - Round 1 |
|---|
| Finished |
Limak has a grid that consists of 2 rows and n columns. The j-th cell in the i-th row contains an integer ti, j which can be positive, negative or zero.
A non-empty rectangle of cells is called nice if and only if the sum of numbers in its cells is equal to 0.
Limak wants to choose some nice rectangles and give them to his friends, as gifts. No two chosen rectangles should share a cell. What is the maximum possible number of nice rectangles Limak can choose?
The first line of the input contains an integer n (1 ≤ n ≤ 300 000) — the number of columns in the grid.
The next two lines contain numbers in the grid. The i-th of those two lines contains n integers ti, 1, ti, 2, ..., ti, n ( - 109 ≤ ti, j ≤ 109).
Print one integer, denoting the maximum possible number of cell-disjoint nice rectangles.
6
70 70 70 70 70 -15
90 -60 -30 30 -30 15
3
4
0 -1 0 0
0 0 1 0
6
3
1000000000 999999999 -1000000000
999999999 -1000000000 -999999998
1
In the first sample, there are four nice rectangles:
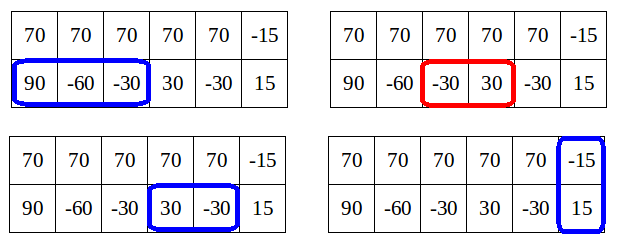
Limak can't choose all of them because they are not disjoint. He should take three nice rectangles: those denoted as blue frames on the drawings.
In the second sample, it's optimal to choose six nice rectangles, each consisting of one cell with a number 0.
In the third sample, the only nice rectangle is the whole grid — the sum of all numbers is 0. Clearly, Limak can choose at most one nice rectangle, so the answer is 1.
| Name |
|---|




