The presidential election is coming in Bearland next year! Everybody is so excited about this!
So far, there are three candidates, Alice, Bob, and Charlie.
There are n citizens in Bearland. The election result will determine the life of all citizens of Bearland for many years. Because of this great responsibility, each of n citizens will choose one of six orders of preference between Alice, Bob and Charlie uniformly at random, independently from other voters.
The government of Bearland has devised a function to help determine the outcome of the election given the voters preferences. More specifically, the function is 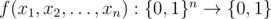 (takes n boolean numbers and returns a boolean number). The function also obeys the following property: f(1 - x1, 1 - x2, ..., 1 - xn) = 1 - f(x1, x2, ..., xn).
(takes n boolean numbers and returns a boolean number). The function also obeys the following property: f(1 - x1, 1 - x2, ..., 1 - xn) = 1 - f(x1, x2, ..., xn).
Three rounds will be run between each pair of candidates: Alice and Bob, Bob and Charlie, Charlie and Alice. In each round, xi will be equal to 1, if i-th citizen prefers the first candidate to second in this round, and 0 otherwise. After this, y = f(x1, x2, ..., xn) will be calculated. If y = 1, the first candidate will be declared as winner in this round. If y = 0, the second will be the winner, respectively.
Define the probability that there is a candidate who won two rounds as p. p·6n is always an integer. Print the value of this integer modulo 109 + 7 = 1 000 000 007.
The first line contains one integer n (1 ≤ n ≤ 20).
The next line contains a string of length 2n of zeros and ones, representing function f. Let bk(x) the k-th bit in binary representation of x, i-th (0-based) digit of this string shows the return value of f(b1(i), b2(i), ..., bn(i)).
It is guaranteed that f(1 - x1, 1 - x2, ..., 1 - xn) = 1 - f(x1, x2, ..., xn) for any values of x1, x2, ldots, xn.
Output one integer — answer to the problem.
3
01010101
216
3
01101001
168
In first sample, result is always fully determined by the first voter. In other words, f(x1, x2, x3) = x1. Thus, any no matter what happens, there will be a candidate who won two rounds (more specifically, the candidate who is at the top of voter 1's preference list), so p = 1, and we print 1·63 = 216.
| Name |
|---|




