| Educational Codeforces Round 30 |
|---|
| Finished |
Merge sort is a well-known sorting algorithm. The main function that sorts the elements of array a with indices from [l, r) can be implemented as follows:
- If the segment [l, r) is already sorted in non-descending order (that is, for any i such that l ≤ i < r - 1 a[i] ≤ a[i + 1]), then end the function call;
- Let
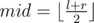 ;
; - Call mergesort(a, l, mid);
- Call mergesort(a, mid, r);
- Merge segments [l, mid) and [mid, r), making the segment [l, r) sorted in non-descending order. The merge algorithm doesn't call any other functions.
The array in this problem is 0-indexed, so to sort the whole array, you need to call mergesort(a, 0, n).
The number of calls of function mergesort is very important, so Ivan has decided to calculate it while sorting the array. For example, if a = {1, 2, 3, 4}, then there will be 1 call of mergesort — mergesort(0, 4), which will check that the array is sorted and then end. If a = {2, 1, 3}, then the number of calls is 3: first of all, you call mergesort(0, 3), which then sets mid = 1 and calls mergesort(0, 1) and mergesort(1, 3), which do not perform any recursive calls because segments (0, 1) and (1, 3) are sorted.
Ivan has implemented the program that counts the number of mergesort calls, but now he needs to test it. To do this, he needs to find an array a such that a is a permutation of size n (that is, the number of elements in a is n, and every integer number from [1, n] can be found in this array), and the number of mergesort calls when sorting the array is exactly k.
Help Ivan to find an array he wants!
The first line contains two numbers n and k (1 ≤ n ≤ 100000, 1 ≤ k ≤ 200000) — the size of a desired permutation and the number of mergesort calls required to sort it.
If a permutation of size n such that there will be exactly k calls of mergesort while sorting it doesn't exist, output - 1. Otherwise output n integer numbers a[0], a[1], ..., a[n - 1] — the elements of a permutation that would meet the required conditions. If there are multiple answers, print any of them.
3 3
2 1 3
4 1
1 2 3 4
5 6
-1
| Name |
|---|




