1208A — XORinacci
The sequence is $$$a$$$, $$$b$$$, $$$a\oplus b$$$, $$$a$$$, $$$b$$$, $$$a\oplus b$$$ $$$\cdots$$$
Since, the sequence has a period of $$$3$$$, $$$f[i] = f[i \mod 3]$$$.
1208B — Uniqueness
After removing a sub-segment, a prefix and a suffix remain, possibly of length $$$0$$$. Let us fix the prefix which does not contain any duplicate elements and find the maximum suffix we can get without repeating the elements. We can use map/set to keep track of the elements.
Time complexity: $$$O(n^2 \cdot log(n))$$$
1208C — Magic Grid
Divide the grid into four quadrants. Assign distinct integers to the first quadrant from $$$0$$$ to $$$(\frac{N^2}{4} - 1)$$$. Copy this quadrant to the other three. This way XOR of each row and column becomes $$$0$$$.
Now, to make numbers distinct among the quadrants, multiply the numbers by $$$4$$$. Add $$$1$$$, $$$2$$$, and $$$3$$$ to the numbers in $$$1^{st}$$$, $$$2^{nd}$$$ and $$$3^{rd}$$$ quadrants respectively. The XOR of each row and column would still remain $$$0$$$ as $$$N/2$$$ is also even but the elements will become distinct while being in the range $$$[0, N^2-1].$$$
Another approach in this problem is to use a $$$ 4 \times 4$$$ grid given in the sample itself and replicate it in $$$N \times N$$$ grid by adding $$$16, 32, 48 \cdots $$$ to make the elements distinct.
Of course, there are multiple ways to solve the problem. These are just a few of them.
1208D — Restore Permutation
Approach 1
Let us fill the array with numbers from $$$1$$$ to $$$N$$$ in increasing order.
$$$1$$$ will lie at the last index $$$i$$$ such that $$$s_{i} = 0$$$. Find and remove this index $$$i$$$ from the array and for all indices greater than $$$i$$$, reduce their $$$s_{i}$$$ values by $$$1$$$. Repeat this process for numbers $$$2, 3, ...N$$$. In the $$$i^{th}$$$ turn, reduce the elements by $$$i$$$.
To find the last index with value zero, we can use segment tree to get range minimum query with lazy propagation.
Time complexity: $$$O(N \cdot log(N))$$$
Approach 2
For every i from $$$N$$$ to 1, let's say the value of the $$$s_{i}$$$ is x. So it means there are $$$k$$$ smallest unused numbers whose sum is $$$x$$$. We simply put the $$$k+1$$$st number in the output permutation at this $$$i$$$, and continue to move left. This can be implemented using BIT and binary lifting.
Thanks to real.emerald for expressing the solution in the above words.
1208E — Let them slide
For every array $$$i$$$ from $$$1$$$ to $$$N$$$, let us maintain 2 pointers $$$L[i]$$$ and $$$R[i]$$$, representing the range of elements in $$$i_{th}$$$ array, that can be accessed by the current column index $$$j$$$.
Initially all $$$L[i]$$$ and $$$R[i]$$$ would be set equal to 0.
As we move from $$$j_{th}$$$ index to $$$(j+1)_{th}$$$ index, some $$$L[i]$$$ and $$$R[i]$$$ would change. Specifically, all those arrays which have $$$size \ge min(j,W-j-1)$$$ would have their $$$L[i]$$$ and $$$R[i]$$$ change.
Since overall movement of $$$L[i]$$$ and $$$R[i]$$$ would be equal to $$$2 \cdot$$$ size_of_array($$$i$$$). Overall change would be of order of $$$O(\sum a[i])$$$. For every array we need range max query in $$$(L[i], R[i])$$$.
We can use multisets/ segment trees/ deques to update the answers corresponding to an array if its $$$L[i], R[i]$$$ changes. This way we can get complexity $$$O(N)$$$ or $$$O(N \cdot log(N))$$$ depending upon implementation.
1208F — Bits And Pieces
The idea is to first fix some $$$a[i]$$$ and try to get the bits which are off in $$$a[i]$$$ from any $$$2$$$ elements to the right of $$$i$$$. Since, we need to maximize the value, we will try to get higher bits first. What we need now is, for every number $$$x$$$ from $$$0$$$ to $$$2^{21}-1$$$, the $$$2$$$ right most positions such that the bits present in $$$x$$$ are also present in the elements on those positions. This can be done by iterating over submasks(slow) or SOS-DP(fast).
Once we process the positions for every $$$x$$$, let us fix some $$$a[i]$$$ and iterate over the bits which are off in $$$a[i]$$$ from the highest to the lowest. Lets say the current maximum we have got is $$$w$$$ and we are going to consider the $$$y^{th}$$$ bit. We can get this bit if the $$$2$$$ positions for $$$w|2^{y}$$$ are to the right of $$$i$$$ else we can not.
The final answer would be the maximum of $$$a[i]|w$$$ over all $$$i$$$ from $$$1$$$ to $$$N$$$.
Time complexity $$$O((M+N)\cdot logM)$$$ where $$$M$$$ is the max element in the array.
1208G — Polygons
If we choose a polygon with side length $$$l$$$, it is profitable to choose polygons with side lengths as divisors of $$$l$$$ as well, because this will not increase the answer.
So our final set would be such that for every polygon with side length $$$l$$$, we would have polygons with side length as divisors of $$$l$$$ as well.
All polygons should have at least one common point in the final arrangement, say $$$P$$$ or else we can rotate them and get such $$$P$$$. For formal proof, please refer this comment by orz.
Let us represent points on the circle as the distance from point $$$P$$$. Like for $$$k$$$ sided polygon, $$$0$$$,$$$\frac{1}{k} ,\frac{2}{k} ,…\frac{k-1}{k}$$$.
Now the number of unique fractions over all the polygons would be our answer, which is equal to sum of $$$ \phi (l)$$$ over all side lengths $$$l$$$ of the polygons because for $$$l$$$ sided polygon there will be $$$\phi(l)$$$ extra points required by it as compared to its divisors.
One observation to get to the final solution is $$$\phi(l) \ge \phi(divisor(l))$$$. So, we can sort the side lengths by their $$$\phi$$$ values and take the smallest $$$k$$$ of them. This will minimize the number of points as well as satisfy the property of our set.
NOTE: We can not consider polygon of side length $$$2$$$. This can be handled easily.










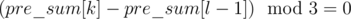
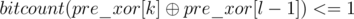
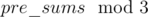 in a
in a 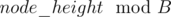 and then taking the index corresponding to the minimum value as
and then taking the index corresponding to the minimum value as 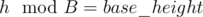 will be marked special. Hence there can be at most
will be marked special. Hence there can be at most 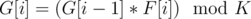
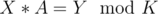 , for some
, for some 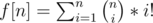 , where
, where 

