703A — Mishka and Game
In this problem you had to do use the following algo. If Mishka wins Chris in the current round, then increase variable countM by 1. Otherwise (if Chris wins Mishka) increase variable countC. After that you had to compare this values and print the answer.
703B — Mishka and trip
Let's look at the first capital. Note that the total cost of the outgoing roads is c[id1] · (sum - c[id1]), where sum — summary beauty of all cities. Thus iterating through the capitals we can count the summary cost of roads between capitals and all the other cities. But don't forget that in this case we count the roads between pairs of capitals twice. To avoid this on each step we should update sum = sum - c[idcur] , where idcur is the position of current capital. In the end we should add to the answer the cost of roads between "non-capital" neighbour cities.
Complexity — O(n).
703C — Chris and Road
Imagine that the bus stands still and we move "to the right" with a constant speed v. Then it's not hard to see that movement along the line y = (u / v) · (x - v · t0) is optimal, where t0 — time in which we begin our movement. In this way answer is t = t0 + (w / u).
If t0 = 0, then we start our movement immediately. In this case we need to check that our line doesn't intersect polygon (either we can cross the road in front of a bus, or the bus is gone).
Otherwise we need to find such minimal t0 that our line is tangent to the polygon. It can be done with binary search.
Complexity — O(n log n).
Exercise: Solve this problem in O(n).
703D — Mishka and Interesting sum
Easy to see, that the answer for query is XOR-sum of all elements in the segment xored with XOR-sum of distinct elements in the segment. XOR-sum of all numbers we can find in O(1) using partial sums. As for the XOR-sum of distinct numbers... Let's solve easier problem.
Let the queries be like "find the number of distinct values in a segment". Let's sort all the queries according to their right bounds and iterate through all elements of our array. We also need to make a list last, where last[value] is the last position of value on the processed prefix of array. Assume we are at position r. Then the answer for the query in the segment [l, r] (l ≤ r) is 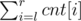 , where cnt[i] = 1 if last[ai] = i and 0 otherwise. It's easy to store and update such values in cnt. When moving to the next position we have to make the following assignments: cnt[last[ai]] = 0, cnt[i] = 1, last[ai] = i. To get described sum in O(log n) we can use segment tree (or Fenwick tree) instead of standard array.
, where cnt[i] = 1 if last[ai] = i and 0 otherwise. It's easy to store and update such values in cnt. When moving to the next position we have to make the following assignments: cnt[last[ai]] = 0, cnt[i] = 1, last[ai] = i. To get described sum in O(log n) we can use segment tree (or Fenwick tree) instead of standard array.
Now let's turn back to our problem. Everything we have to do is to change assignment cnt[i] = 1 to cnt[i] = ai and count XOR-sum instead of sum. Now we can solve this problem in O(n log n).
P.S.: Also there is a solution with O(n sqrt n) complexity (using Mo's algo), but we tried to kill it :D
703E — Мишка и делители
Let's use dp to solve this problem.
Suppose dp[i][d] is the minimal number of elements on prefix of size i, that their product is divisible by d. It's easy to see that dp[i][d] = min(dp[i - 1][d], dp[i - 1][d / gcd(d, ai)] + 1). That is so because it's optimal to take as much divisors of ai as possible. Answer — dp[n][k].
Let's imrove our solution. Notice, that as d we should use only divisors of k (which in the worst case would be 6720). As for gcd, we can easily find it in O(primes(k)), where primes(k) — number of primes in decomposition of k. We also need to renumber our divisors according to their prime decomposition.
To get AC in this problem you had to optimize described dp and add minimization of used elements' sum. Final complexity — O(n · divs(k) · primes(k)).










